Перспективные режимы Sponge-шифрования
Конструкция Sponge ранее рассматривалась в обзоре совместно с алгоритмом Keccak, благодаря которому она и получила наибольшую известность. С того момента Keccak стал победителем конкурса на стандарт хэширования SHA-3. Но, как ранее отмечалось, конструкция Sponge и построенный на ней алгоритм Keccak — это не просто хэш, а универсальный симметричный криптопримитив, позволяющий решать множество разных задач. В данном обзоре мы более подробно рассмотрим возможности Sponge для шифрования.
Вспомним, как устроена конструкция Sponge в общем виде (см. рис. 1).
Стартовый блок b (на схеме разделён на части r и c) состоит из одних нулей. Исходное сообщение M дополняется до нужного размера блока, равного части блока b, т.е. r и разделяется для поблочной обработки. Каждый такой блок сообщения M объединяется с частью r блока b при помощи операции XOR. Между этими объединениями и в заключительной части после них, блоки обрабатываются функцией многораундовой бесключевой перестановки f. Все эти преобразования входят в стадию поглощения (абсорбции) сообщения.
Во второй стадии происходит обратный процесс: стадия отжатия псевдослучайного потока данных, выработанных на основе поглощённого сообщения. Для этого из каждой части блока r выводится блок исходящих данных, между всеми блоками также производится обработка всего внутреннего состояния функцией f как и в первой стадии. Накопленные блоки формируют исходящие данные Z.
Важно отметить, что в часть c никакие данные напрямую не вводятся и не выводятся из неё. Она только перемешивается с частью r блока b при помощи функции f.
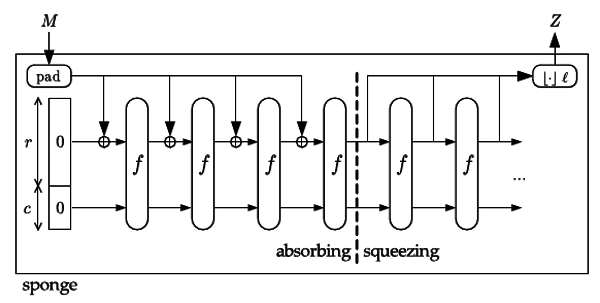
Рис. 1. Общий вид конструкции Sponge.
В простейшем случае M — это любое сообщение, а Z — это его псевдослучайное отображение. Т.е. функция Sponge работает в режиме хэш-функции.
Если перед блоками сообщения ввести блок с секретным ключом K, то получится код аутентификации сообщения (Message Authentication Code — MAC). Полученный с таким ключом проверочный хэш-код иногда кратко называется тэг (Tag), как показано на рис. 2:
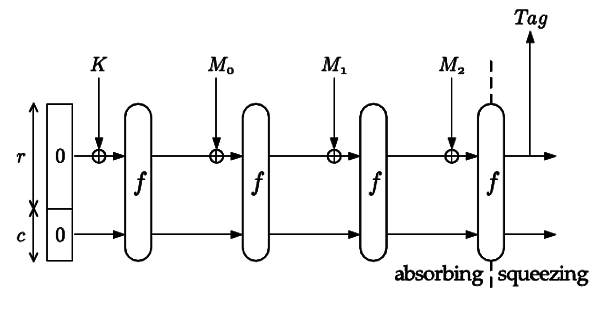
Рис. 2. Функция Sponge в режиме MAC.
При помощи знания секретного K и тэга можно аутентифицировать сообщение — удостовериться, что его отправил только тот, кто знает K и что сообщение никто не исказил в процессе хранения и/или передачи: иначе вычисленный и присланный вместе с сообщением Tag не сойдутся, а без знания K противник не сможет подделать корректный Tag к подложному сообщению.
Можно использовать Sponge и для шифрования. Для этого на вход в стадии сжатия нужно вместо сообщения подать ключ шифрования K, объединённый с вектором инициализации (уникальным несекретным случайным значением N — nonce, передаваемым открыто). Тогда в стадии отжатия псевдослучайные данные на выходе с блоков можно рассматривать как гамму потокового шифра и объединять при помощи операции XOR с блоками сообщения M, как показано на рис. 3:
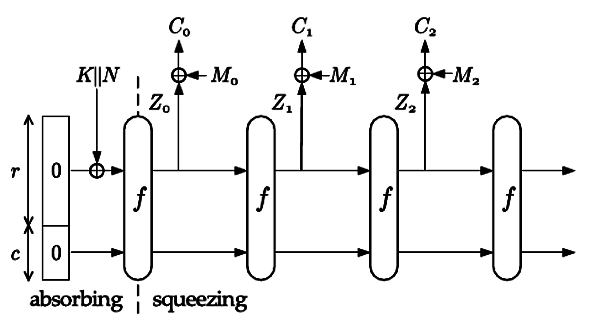
Рис. 3. Шифрование Sponge.
При этом такой режим шифрования является неаутентифицированным. Даже если противник не знает секретный ключ K, он может инвертировать любой бит в шифртексте, что приведёт к инвертированию бита в открытом тексте. Поскольку открытый текст часто является структурированным и предсказуемым (например поле с суммой денежной транзакции), то противник может модифицировать шифртекст нужным ему образом для того, чтобы получатель при расшифровании получил подложный открытый текст.
Для этого шифрование обязательно применяют совместно с аутентификацией. При традиционном подходе это достаточно накладно и громоздко: нужно иметь два разных ключа для шифрования и аутентификации и использовать два разных алгоритма. В Sponge алгоритмы похожи, да и вывести производные ключи из одного общего несложно, но можно сделать шифрование и аутентификацию за один проход.
Как показано на рис.4 для этого достаточно операцией XOR сообщение M объединять с выходом гаммы, а затем снова вводить в функцию Sponge при помощи операции XOR. Все данные будут поблочно зашифрованы, а в конце будет выведен MAC — Tag. Из-за нелинейности функции f повреждение в шифртексте приведёт к изменению внутреннего состояния функции Sponge, что приведёт к искажению всех последующих блоков шифртекста и несовпадению значения Tag.
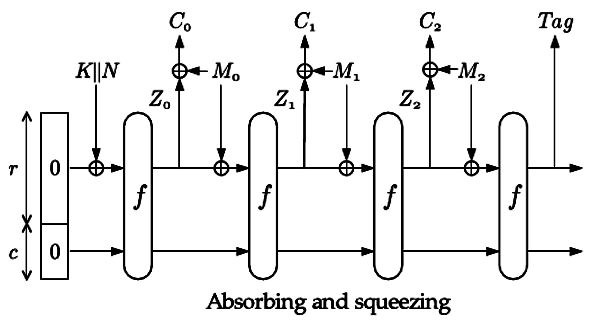
Рис. 4. Шифрование с аутентификацией Sponge.
Поскольку при таком подходе стадии (фазы) поглощения и отжатия чередуются поблочно, то каждые две такие фазы образуют дуплекс, а сам такой режим работы функции Sponge назван дуплексным. В общем виде такой режим показан на рис. 5
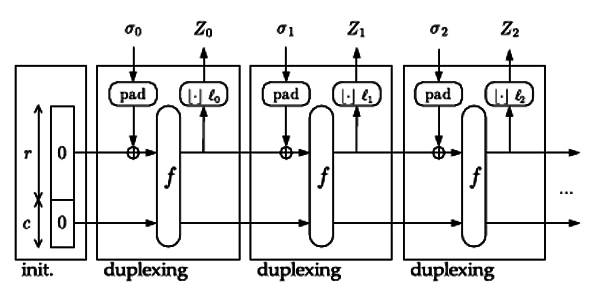
Рис. 5. Дуплексный режим Sponge.
В этом рисунке неспроста вместо сообщений, ключей и тэгов обозначения указывают на абстрактные множества входа и выхода дуплексов. Ведь такой режим может использоваться не только для аутентифицированного шифрования за один проход. Например, на вход дуплекса могут подаваться сырые данные генератора случайных чисел, а с выхода сниматься обработанные. При этом помимо того, что внутреннее состояние на каждом блоке выходит не всё (только часть r), но и передаётся на следующий дуплекс (совместно с секретной часть c), то это позволяет строить простые и эффективные сборщики энтропии для генераторов псевдослучайных чисел со свойством непредсказуемости влево и вправо («наперёд» и «назад» заданной секретностью). Для подстраховки от недостаточного качества входящей энтропии может использоваться дуплекс, в котором количество блоков в фазе абсорбции больше, чем в фазе отжатия.
Однако, если вернуться к вопросу аутентифицированного шифрования Sponge, то у него остаётся один практический недостаток: оно может исполняться только последовательно и не может исполняться параллельно. Ранее считалось, что такие параллельные режимы возможны только для блочных шифров (OCB, GCM) или при использовании громоздкого режима древовидного хэширования.
Но исследователи Павел Моравецки (Отделение информатики университета коммерции Кельце, Польша) и Йозеф Пиепжик (Кафедра компьютерных наук, Университет Маккуори, Австралия) предложили простой, очевидный и эффективный способ параллельного исполнения аутентифицированного Sponge-шифрования.
Вариант схемы этого режима показан на рис. 6.
Ключ объединяется с вектором инициализации (Nonce) и подаётся на вход множества параллельных конструкций Sponge, где предварительно объединяется ещё и со значением счётчика каждой Sponge-конструкции. Также на вход Sponge могут быть поданы блоки персонифицируещего сообщения A (для простоты его можно вообще не рассматривать — оно предназначено для добавления несекретных параметров к ключу, например в процессе менеджмента ключей для избежания их ошибочного использования).
Затем блоки открытого текста (на данной схеме B) проходят через дуплекс, формируя блоки шифртекста C и выводя промежуточные тэги аутентификации t на выходе из каждой Sponge-конструкции. Тэги t объединяются операцией XOR, формируя общий тэг аутентификации T. Понятно, что порядок выполнения Sponge-конструкций и XOR-объединения промежуточных тэгов t не играет никакой роли, поэтому весь режим может быть эффективно распараллелен.
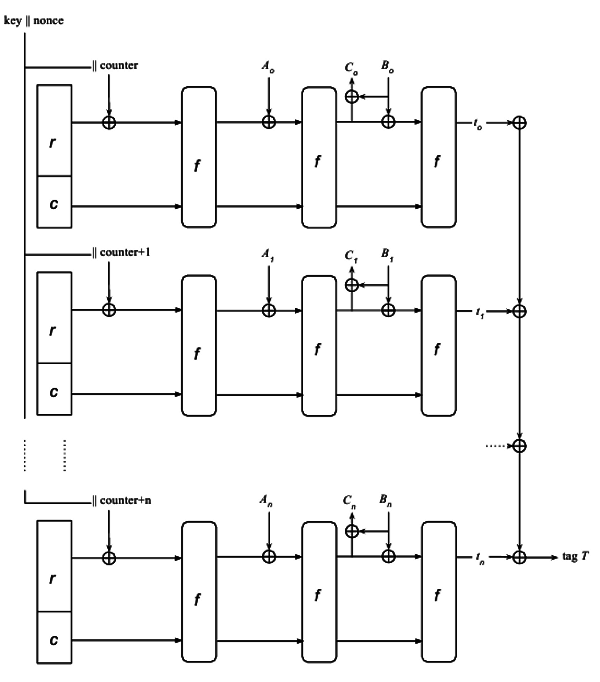
Рис. 6. Параллельное шифрование с аутентификацией Sponge.
Таким образом, вместо некоторых патентованных и легкоуязвимых при неправильном исполнении режимов аутентифицированного шифрования на блочных шифрах, появляется возможность использовать Keccak/Sponge в параллельном режиме. Это существенным образом упрощает создание протоколов, требующих шифрования с аутентификацией (а такие чаще всего встречаются на практике) и избавляет от множества потенциальных ошибок в их проектировании и реализации.
Единственное, чего не хватает алгоритму Keccak для того, чтобы нести звание полноценного универсального криптопримитива — это возможности использовать его в качестве блочного шифра, что было бы полезно, например, в режимах дискового шифрования. Но, во-первых, создание такого режима не исключается. А во-вторых, существуют экспериментальные разработки стойкого дискового шифрования на основе потоковых шифров (псевдослучайных функциях, PRF), вместо блочных шифров (псевдослучайных перестановках, PRP). И функция Sponge ещё не раскрыла весь свой потенциал в создании новых режимов.
Следует ли при этом опасаться того, что почти вся криптография окажется построена на одном алгоритме, что может привести к единой точке отказа в случае его взлома?
Против этого можно привести ряд таких аргументов:
- Вместо алгоритма Keccak в виде функции Sponge может быть реализован любой другой алгоритм бесключевой перестановки f с подходящим размером внутреннего состояния.
- Все режимы использования функции Sponge имеют простую и прозрачную возможность обоснования стойкости в модели случайного оракула в случае неразличимости функции f от идеальной псевдослучайной перестановки. В то же время, неуниверсальные алгоритмы требуют гораздо больше допущений и контроля возможности появления неучтённых свойств при их сочетании.
- В большинстве современных протоколов (и в ряде случаев режимов использования алгоритмов) существуют изъяны в доказательствах стойкости из-за смешения разных базовых криптопримитивов. Это приводит к неизбежным ошибкам из-за сложностей в их правильной реализации.
- В случае взлома какого-либо из фундаментальных криптопримитивов, используемых сейчас раздельно в составе более общего протокола (блочный шифр, потоковый шифр, хэш-функция), многие включающие их протоколы всё равно окажутся нестойкими и попытка перестраховки на смешении алгоритмов мало спасёт ситуацию.
Литература:
"![]() Permutation-based encryption, authentication and authenticated encryption". Joan Daemen, Michaёl Peeters, Gilles Van Assche, Guido Bertoni. DIAC 2012, Stockholm, July 6., см. также
Permutation-based encryption, authentication and authenticated encryption". Joan Daemen, Michaёl Peeters, Gilles Van Assche, Guido Bertoni. DIAC 2012, Stockholm, July 6., см. также ![]() слайды.
слайды.
"![]() Duplexing the sponge: single-pass authenticated encryption and other applications". Guido Bertoni, Joan Daemen, Michaлl Peeters, Gilles Van Assche (STMicroelectronics, NXP Semiconductors).
Duplexing the sponge: single-pass authenticated encryption and other applications". Guido Bertoni, Joan Daemen, Michaлl Peeters, Gilles Van Assche (STMicroelectronics, NXP Semiconductors).
"Parallel authenticated encryption with the duplex construction". Pawel Morawiecki (Section of Informatics, University of Commerce, Kielce, Poland), Josef Pieprzyk (Department of Computing, Macquarie University, Australia).


