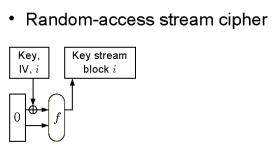
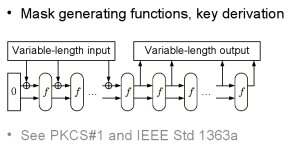
Хэш-функция Keccak и конструкция Sponge как универсальный криптопримитив

Кризис в области криптографии, связанный со стойкостью хэш-функций, наиболее ярко проявившийся в середине 2000-х годов, вынудил американский институт стандартов и технологий (НИСТ) объявить конкурс на создание нового стандарта хэширования — SHS (Secure Hash Standart). Победитель конкурса алгоритмов хэширования получит имя хэш-функции SHA-3.

В ходе конкурса получили распространение, широкое обсуждение и значительное принятие различные идеи, связанные с дизайном как самих хэш-функций, так и симметричных криптопримитивов в целом.

Особенно интересным явлением стало то, что в финале конкурса из пяти финалистов, двое оказались универсальными криптопримитивами, которые могут использоваться не только для хэширования, но и для выполнения множества других криптографических операций. Это может привести на практике к значительному упрощению криптографических протоколов, как уже существующих, так и вновь проектируемых.

О другом универсальном криптопримитиве Skein было подробно написано ранее. Тем интереснее также подробно разобрать Keccak и сравнить его со Skein. Следует сразу отметить, что Keccak (в отличие от Skein) не содержит в своей основе блочный шифр и поэтому не является совсем универсальным. Однако, в других областях его гибкость и универсальность проявляются достаточно полно. В ряде случаев он может например использоваться в таких протоколах, в которых нужно использование блочного шифра в режиме счётчика.

Традиционный дизайн хэш-функций основан на использовании функции сжатия. Эта функция отображает значение m → n (m > n) псевдослучайным образом. При этом значение n должно быть до 512 бит, а m порядка 2n. Повторяя эту функцию в течении нескольких раундов с различными константами, достигают нужного значения стойкости. Дополняя и сцепляя между собой блоки от разных фрагментов исходного текста, получают возможность вычислить хэш от сообщения произвольной длины. При этом возникает существенная проблема: сконструировать функцию сжатия трудно. Многораундовые повторения сгладят её дефектность, но заведомое наличие быстрой возможности найти частичную коллизию в исходной функции сжатия ставит под вопрос стойкость всей конструкции. Авторы алгоритма Keccak (Guido Bertoni, Joan Daemen, Michaёl Peeters и Gilles Van Assche) утверждают, что сконструировать надёжную функцию сжатия вида m → n (m > n) как однораундовый блок криптопримитива, крайне сложно (или невозможно вообще).

Авторы алгоритма Skein (и Whirlpool, который не участвует в конкурсе, но вошёл в некоторые промежуточные стандарты) считают, что в качестве функции сжатия можно использовать блочный шифр. Действительно, в отличие от псевдослучайных функций (Pseudo Random Function — PRF), псевдослучайные перестановки (Pseudo Random Permutation — PRP), создавать проще. А блочный шифр является такой перестановкой, зависимой от ключа. Достаточно сконструировать шифр с размером блока и размером ключа 512 бит и можно будет получить функцию сжатия m → n (m > n), подавая на вход такого шифра эти значения. Проблема однако в том, что хотя блочные шифры и считаются самыми доверяемыми в плане стойкости симметричными криптопримитивами, они часто имеют облегчённое или слабое ключевое расписание (функцию разворачивания подключей раунда из основного ключа). Это приводит к атакам со связанными ключами, которые хотя и не представляют практической угрозы в большинстве протоколов, но ставят под удар функцию сжатия на основе блочного шифра. Более того — идеальное ключевое расписание для идеального блочного шифра само по себе должно обладать свойствами идеальной псевдослучайной функции. То есть для создания идеальной хэш-функции нужно использовать … идеальную хэш-функцию. Получается замкнутый круг, который лишь отчасти можно победить некоторыми конструкторскими уловками и некоторыми натяжками в доказательствах. Так, можно использовать фиксированный ключ, но изменяющийся твик-вектор или использовать лишь часть выхода шифра.

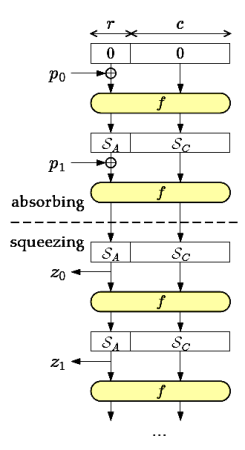
Авторы хэш-функции Keccak (произносится как "Ketchak") приняли ряд радикальных решений. Они решили не использовать функцию сжатия в виде отдельного строительного блока, а в качестве стойкого криптопреобразования решили сконструировать бесключевую PRP. Всё это упаковано в очень простую конструкцию Sponge ("Губка"). Авторами этой конструкции являются непосредственные создатели алгоритма Keccak, которые впервые представили её на симпозиуме ECRYPT Hash function – 2007 в качестве альтернативы традиционному дизайну Дамгарда-Меркла.

В фазе абсорбции ("поглощения", "впитывания" губкой) сначала задаётся исходное состояние из нулевого вектора размером до 1600 бит. Затем производится операция xor фрагмента исходного сообщения p0 с фрагментом исходного состояния размером r, оставшаяся часть состояния ёмкостью c остаётся незатронутой. Результат обрабатывается функцией f — многораудовой бесключевой PRP и так повторяется до исчерпания блоков исходного сообщения. Затем наступает фаза сжатия или отжатия (как если бы отжимали губку), при которой можно вывести хэш произвольной длины. При этом сложность проведения атак гарантируется только до необходимой величины. После увеличения длины выхода хэш-функции за пределы внутреннего состояния, её стойкость перестаёт зависеть от размера выхода.

Атаки на нахождение коллизий (двух произвольных сообщений, дающих одинаковый хэш) и вторых прообразов (сообщения, дающего такой же хэш, что и имеющееся) имеют важное практическое и теоретическое значение, но наряду с неинвертируемостью не обеспечивают полной оценки стойкости хэш-функции. Существует целый ряд экзотических атак — на удлинение сообщения, атаки на частичные коллизии с подобранным префиксом и др. Чтобы доказать стойкость конструкции Sponge ко всем возможным атакам, авторы приняли ещё одно радикальное решение: считать единственным и достаточным общим критерием стойкости неразличимость хэш-функции от случайного оракула.

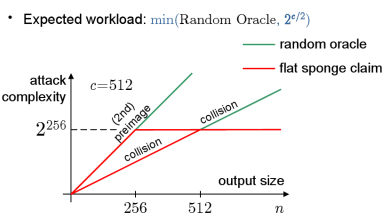
Случайный оракул (Random Oracle) — это идеализированная функция, описывающая работу машины с практически бесконечным объёмом памяти, которая на любой запрос может выдать идеально случайное число и запомнить пару "запрос-ответ". Если такой же запрос будет когда-либо повторён, то ответ будет не генерироваться заново, а взят из запомненного списка. Если перестановка f, лежащая в основе Sponge идеальна, то и хэш-функция доказуемо неразличима от RO, значит никакие из возможных атак действовать не будут. Конечно, есть оговорка на наличие универсального тривиального различителя для всех возможных хэш-функций: построение случайного оракула на алгоритме с конечным числом состояний невозможно. Например коллизия внутреннего состояния приведёт к неслучайному выходу, что было бы невозможно в RO, у которого никаких внутренних состояний нет. Однако, авторы доказывают, что такая конструкция обеспечивает стойкость для N запросов к функции f или f^-1, равную N² • 2^-(c+1), что при обычной длине выхода укладывается в 2^c/2 и невозможно без наличия различителя в используемой PRP.

Именно эти теоретические результаты, основанные на одном из самых строгих доказательств неразличимости от случайного оракула в конкурсе SHA-3, дают удивительные практические возможности для простого использования хэш-функции Keccak в качестве практически универсального криптопримитива.

	Простое добавление секретного ключа на вход хэш-функции Keccak/Sponge превращает её в код аутентификации сообщений. Это было невозможно в обычных хэш-функциях SHA-1 или SHA-2 и требовало громоздкой конструкции HMAC.
	Добавление секретного ключа с открытым вектором инициализации и вывод гаммы произвольной длины превращает конструкцию Sponge в потоковый шифр.
	Добавление на вход ключа, вектора инициализации и номера блока позволяет получить потоковый шифр с произвольным доступом — аналог блочного шифра в режиме счётчика (AES-CTR). Это может быть использовано совместно с MAC для шифрования сообщений или пакетов данных.
	Использование входа и выхода переменной длины может применяться для генерации симметричных ключей из паролей, из протоколов согласования ключа по асимметричным алгоритмам, для связывания сообщения с электронной подписью, рэндомизированного хэширования, для дистилляции случайных данных из шумов. Если периодически уничтожать использованные предыдущие состояния, то из такой конструкции легко построить генератор псевдослучайных чисел.

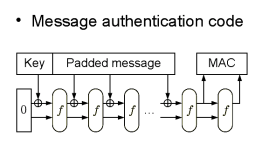
Ещё одной интересной особенностью конструкции Sponge является лёгкость персонализации данных. Предположим, один и тот же пароль используется как для генерации симметричного ключа, так и для ключа MAC — для предотвращения изменения сообщения. Нежелательно, чтобы они были одинаковыми. Например, в хэш-функции Skein для этого предусмотрен ограниченный набор битов для переключения режимов использования. А в конструкции Sponge хэш-функции Keccak это не требуется. Любая персонализация данных может быть добавлена на вход функции, например, по рекомендации авторов, в XML-формате и кодировке UTF, что делает число возможных вариантов персонализации и режимов использования практически неограниченным.

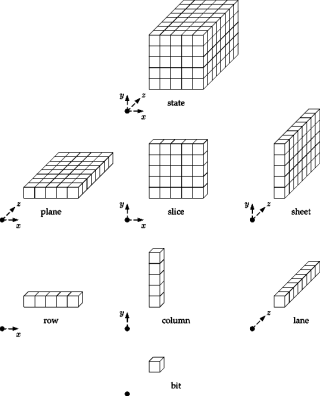Кроме конструкции Sponge, интересна также и сама функция перестановки хэш-функции Keccak. Текущее внутреннее состояние представлено в ней в виде набора битов, сгруппированных в виде виртуального объекта в трёхмерном пространстве (трёхмерного массива). Сам объект можно разбить на плоскости или точнее слои вдоль трёх осей координат, а элементы каждого слоя — на фрагменты в виде столбцов или векторов. При этом для обработки внутренних состояний не используются S-блоки или операции, параметры которых менялись бы в зависимости от данных. Для создания нелинейных преобразований используется набор простейших логических операций (XOR, AND, NOT), которые существуют в любом процессоре и минимальный набор констант. А трёхмерное представление текущего внутреннего состояния помогает применить эти операции оптимальным образом. Функции Chi, Theta, Pi, Rho и Iota последовательно обрабатывают внутреннее состояние на каждом раунде. На странице Олденбургского университета имени Карла фон Осиетски представлено описание этих функций на немецком языке и анимированные диаграммы состояний. Чтобы не разбирать подробно процесс их работы, можно посмотреть по приведённой ссылке анимированные изображения в gif-формате, которые позволяют понять работу алгоритма наглядным образом.

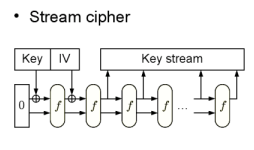
Таким образом, хэш функция Keccak является почти таким же универсальным криптопримитивом, как и Skein, за исключением возможности использования в режиме блочного шифра. Режим блочного шифра остаётся незаменимым в прозрачном шифровании данных на дисках компьютеров, но в этой области нет существенного ограничения по ресурсам, поэтому для шифрования можно использовать отдельный блочный шифр в соответствующем режиме. Для решения же многих других задач Keccak также универсален, как и Skein, а фактически его область применения может быть шире. При необходимости этот алгоритм мог бы быть легко внедрён как в миниатюрные устройства с ограниченными ресурсами, так и на высокопроизводительные серверы, работающие с большим объёмом соединений. Оба алгоритма имеют самую сильную доказательную базу среди всех финалистов, но по некоторым оценкам, Keccak имеет более строгие доказательства в модели RO. В частности он неподвержен атакам на функции конструкции Narrow Pipe.

В случае принятия любого из этих достойных кандидатов (как Keccak, так и Skein) в качестве стандарта алгоритма хэширования, на практическое использование симметричных алгоритмов и смешанных протоколов, а также и на теоретические исследования в различных областях криптографии будет оказано заметное стимулирующее влияние.

См. также: Перспективные режимы Sponge-шифрования.