Регистрация10.08 // Swap or Not: простейшие блочные шифры претендуют на стойкость
Несмотря на множество предложенных блочных шифров, в их основе лежат только два варианта конструкций: нечто, что по существу выглядит как некоторая разновидность сети Файстеля (напр. DES, FEAL, MARS, RC6) или SP-сеть (Rijndael, Safer, Serpent, Square). Соответствено, в литературе имеется описание того, как можно сконструировать псевдослучайные перестановки (Pseudo Random Permutations — PRP) из псевдослучайных функций (Pseudo Random Functions — PRF) для доказуемо-безопасных сетей Файстеля, так же как и для режимов операций, из которых могут быть созданы SP-сети (сети замены-перестановки на обратимых операциях). Возможно, что никаких других фундаментально отличающихся путей создания блочных шифров просто не существует. Но может быть просто никто не замечал других возможностей.
Исследователи Ви Тан Хо, Филип Рогуэй (Кафедра компьютерных наук Университета Калифорнии, Дэвис, США) и Бен Моррис (Кафедра математики Университета Калифорнии, Дэвис, США) предложили принципиально новую конструкцию создания блочных шифров. Консультантами в работе служили Михир Беллэйр и Терент Спайс. Следует отметить, что Рогуэй и Беллейр — одни из ведущих специалистов в области доказуемой безопасности, поэтому их разработки привлекают заслуженное внимание.
Самым удивительным свойством новых шифров является минималистичная простота. Если не рассматривать реализации ключевого расписания (авторы их не представили, но их создание может быть делом будущего), то весь шифр может уместиться в короткий однострочник, понятный практически любому программисту-любителю. Другим удивительным свойством является использование одной единственной линейной операции – XOR, которая задаёт перестановки, что приводит к созданию нелинейности. Наконец, шифр, основанный на таком прототипе, возможно будет реализован с ничтожными затратами памяти на исполнение.
Для создания новых шифров исследователи предложили конструкцию swap-or-not-сетей. Сложно перевести это столь же коротким термином, как вариант это может быть "перестановка-обмен с исключениями". В основе идеи лежат хорошо известные алгоритмы математики и комбинаторики первой половины XX века, связанные с генерацией перестановок, аналогичных перетасовке карточной колоды. Исследователям удалось привести первичные доказательства, что такие алгоритмы превосходят по соотношению затрат к стойкости обычные алгоритмы конвертирования PRF → PRP, используемые для создания блочных шифров. Помимо этого, такие алгоритмы претендуют на наилучшее решение проблемы шифрования с сохранением длины и формата сообщения (Format-Preserving Encryption — FPE), когда необходимо шифровать данные, имеющие размер меньше блока традиционного шифра, но при этом именно в блочном режиме, а не наложением гаммы. Такая задача может возникнуть при шифровании номеров PIN, социального страхования, записей в базах данных, использовании недвоичных систем счисления, с возможностью как компромисса в сторону пониженной стойкости, так и с сохранением стойкости на обычном уровне.
Несмотря на то, что алгоритм удивительно простой, следует по порядку рассмотреть несколько вариантов — от простого к сложному, хотя каждый из них сам по себе может стать прототипом каких-либо полезных реализаций.
Пусть первое значение X — это n-битовый исходный текст из множества χ = {0,1}n. Пусть на каждом раунде значение X подвергается операции XOR с n-битовым раундовым подключом Ki, результат записывается как X'. Затем следует сравнить, какое значение получилось больше: X или X' и записать большее значение в Xˆ. Затем нужно применить n-битовую функцию раунда Fi(Xˆ), которая является уникальной для каждого раунда и выдаёт псевдослучайную свёртку в виде однобитового значения Fi: {0,1}n → {0,1}. Если выход этой функции равен единице, то X заменяется на X' — на свою парную точку, в противном случае на этом раунде не происходит никаких изменений.
Поскольку операция X → Ki ⊕ X — это инволюция (самообратимое преобразование), то расшифровка происходит простым прохождением раундов в обратном порядке.
К вопросу о конкретной реализации функции Fi мы вернёмся в конце работы, а сейчас рассмотрим более подробно, почему авторы предложили рассматривать блочный шифр, как перетасовку колоды карт.
Если существует некоторый метод по перетасовке колоды N карт, то он определяет соответствующий метод шифрования N точек: достаточно поместить карту на каждую позицию X ∈ [N], где [N] = {0, 1, …, N-1}; перетасовать карты; затем посмотреть на какой позиции оказалась карта, которая изначально была на позиции X. Такую позицию можно назвать шифртекстом Y для X. Случайность, используемая для шифрования, определяется ключом.
Первое, что нужно, чтобы использовать перетасовку карт в качестве вычислительно приемлемого шифра — это требование вычислений с забыванием или рассеянных вычислений, идея которых была высказана Мони Наором. В забывчивой перетасовке можно следить за траекторией одной карты, не обращая внимания на другие карты в колоде. Большинство известных алгоритмов перетасовок таковыми не являются. Наиболее известный алгоритм рассеянной перетасовки — алгоритм Торпа, поэтому он подходит под метод swap-or-not. Вот как он выглядит в качестве перестановки.
Для колоды из N = 2n карт, каждая из которых размещена на позиции X ∈ [N] случайным образом выбирается n-битовый ключ K. Для каждой пары размещений {X, K ⊕ X} подбрасывается монета b для получения одного бита энтропии. Если выпадает "орёл" или бит "1", то X и K ⊕ X меняются местами. Если "0", то ничего не происходит. Используя независимые честные монеты процесс может быть повторён r раундов для достижения требуемого качества перемешивания ("стойкости").
Если алгоритм swap-or-not-перетасовки со второй иллюстрации перевести обратно на язык криптографии, то мы получим первый алгоритм, swap-or-not-шифр. Это лишь разные взгляды на один и тот же процесс. Случайный выбор парных карт, определяемый ключом K в i-той перетасовке, определяется раундовым подключом Ki в шифровании. Случайный бит b, выкидываемый на каждом раунде в перетасовке пары {X, K ⊕ X}, в случае шифрования соответствует Fi(Xˆ).
Теперь рассмотрим этот алгоритм шифрования с обобщённой областью определения:
Вместо того, чтобы использовать операцию XOR, или иначе говоря, группу G = ({0, 1}n, ⊕), алгоритм может быть исполнен на любой конечной абелевой группе G = ([N], +]). Для определённости, пусть элементы этой группы нумеруются с нуля: [N] = {0, …, N – 1}. Если с операцией XOR шифр мог иметь размер блока, равный любой величине степени двойки, то в случае с произвольной группой в этом нет необходимости. Размер блока шифра может быть любым конечным числом, для этого оператор группы можно задать, к примеру, как сложение по модулю N. Нужно лишь выбирать равномерно и случайно значение K из области N, которое также не является степенью двойки, т.е. не относится к {0,1}n. Вместо парных обменов {X, K ⊕ X} будут использоваться обмены {X, K – X}, а для замены выбором будет X' ← ki – X вместо X' ← Ki ⊕ X. Вот и все отличия от первого алгоритма.
Авторы анализируют стойкость своей swap-or-not-конструкции на основании основополагающей работы Любы-Ракоффа, в которой подразумевается, что соответствующие части преобразования выбираются равномерно и однородно. Тогда алгоритм на третьей иллюстрации можно описать как преобразование SN [r, N, +]: k x [N] → [N], в виде блочного шифра E с количеством раундов r, областью определения сообщений [N], указанным оператором группы "+" и где область определения значений ключей включает все возможные подключи K1, …, Kr ∈ [N] и всех возможных раундовых функций F1, …, Fr: [N → {0, 1}]. Таким образом ключ KF для данного шифра состоит из равномерно выбранных раундовых подключей Ki и Fi.
Для оценки стойкости блочного шифра его сравнивают со стойкой псевдослучайной перестановкой ("strong-PRP"). Сложность нахождения различителя между такой перестановкой и блочным шифром определяет уровень защиты от атак с подобранным шифртекстом, которые включают в себя и атаки с известным и подобранным открытым текстом. Для описания такой модели атакующего A, пытающегося взломать блочный шифр E, помещают в один из двух миров. В первом мире атакующий имеет доступ к оракулу EKF(∙) для случайных KF, а также доступ к его обратному (расшифровывающему) оракулу E-1KF(∙). В другом мире атакующий имеет дело с равномерной случайной перестановкой π: [N] → [N], также как и с обратной перестановкой, π-1(∙). Цель атакующего — определить в каком из миров он находится: в мире управляемом сконструированным шифром или в мире, управляемом случайным оракулом, задающим наборы фиксированных случайных перестановок. В общем виде его успех в этом деле описывается вероятностной зависимостью от числа запросов q к определяемому оракулу:
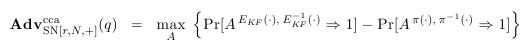
Исследователям удалось вывести конкретное значение, которое равно:
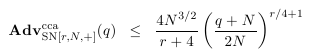
Грубо говоря, достаточно минимум r = 6 lg N раундов swap-or-not для начала хорошего приближения к CCA-стойкости. После этого преимущество противника падает обратно-экспоненциально в зависимости от r. Это превосходит стойкость сетей Файстеля и перестановок Торпа.
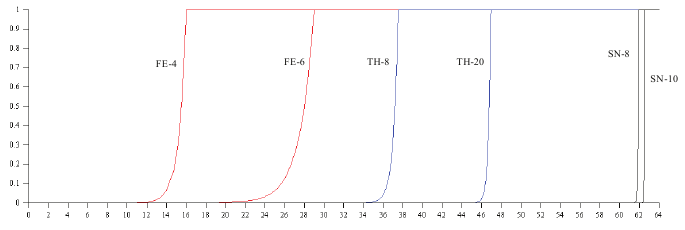
На графике показаны результаты приближения CCA-преимущества для q запросов при N = 264. По оси x значения пронормированы в виде log2(q). Два правых графика показывают результаты шифра swap-or-not с восьмью проходами (512 раундами) (SN-8) и с 10 (SN-10) (один проход определяется как верхнее округление lg N раундов). Для сравнения: два левых графика — это сбалансированная сеть Файстеля по классическим результатам Любы-Ракоффа для четырёх раундов (LR-4) и шестираундовому результату Патарина (LR-6). Посредине показаны перестановки Торпа (TH-8, TH-20).
В качестве простого числового примера, можно показать, что swap-or-not шифрование 64-битных строк за 1200 раундов с использованием случайных раундовых функций позволяет достичь максимального CCA-преимущества менее, чем 10-10, даже если противник может сделать q = 263 запросов. Несмотря на большое число раундов, никакая другая конструкция не обеспечивает безопасность при q близком к N. Кроме того, можно предположить, что раунды swap-or-not будут исполняться эффективнее традиционных сетей Файстеля.
Авторы также приводят вывод информационно-теоретической и комплексно-теоретической оценки стойкости алгоритма.
Однако, можно заметить, что наличие нереализованной идеальной функции F в каждом раунде делает алгоритм слишком теоретическим. Можно ли использовать какую-либо реальную функцию для получения однобитовой свёртки? На этот вопрос авторы отвечают утвердительно.
В качестве такой функции возможно использование двоичного скалярного произведения — цепочки XOR-операций между битами текущего состояния раунда и некоего раундового подключа Li, дающей на выходе один бит:
Используя два раундовых подключа Ki и Li возможно представить полноценный алгоритм:
Здесь отмечается, что использование наибольшего значения max для выбора {X, X'} является обязательным требованием, в противном случае, при использовании минимума, X = 0n всегда будет шифроваться как 0n.
Итак, авторы представили простейший полноценный, обоснованно-стойкий алгоритм блочного шифрования, обладающий свойствами замены и перемешивания (лавинным эффектом), работающий только на операции XOR.
Читатель, знакомый с основами доказуемой безопасности, может почуять подвох в этом месте, о котором говорят сами авторы. При замене идеальной случайной функции F на сконструированную, доказательства стойкости теряют свою строгость и простейшее приближение r = 6n (например 6 ∙ 128 = 768 раундов) не может быть применено.
Однако, такая же проблема существует и в любом другом блочном шифре, который опирается не на признанно сложные математические задачи, а искусственные инженерные построения, поэтому для дальнейшего исследования стойкости с целью определения необходимого числа раундов необходимо определить, насколько выбор реальной функции F для замены её идеализированного представления влияет на стойкость шифра, в частности изучением алгебраической сложности получающихся преобразований. Авторы призывают всех заинтересовавшихся криптографов продолжить исследования в данной области.
В работе не отмечены варианты построения ключевого расписания (разворачивание раундовых подключей из основного ключа), которое подошло бы к таким шифрам. И в этом также может оказаться одна из проблем. Большое количество требуемых раундов исполнения алгоритма возможно сделает непрактичным просчёт всех раундовых подключей и сохранение их в памяти. А попытка создать такой же простой алгоритм ключевого расписания, исполняющийся без предвычислений и затрат памяти — "на лету", может потребовать слишком большого количества операций на каждый подключ.
Тем не менее, интересно запомнить алгоритм построения простейшего универсального блочного шифра, котрый претендует на переворот многих представлений в области симметричной криптографии. Сформулируем его ещё раз простыми словами для удобства запоминания:
- Провести операцию XOR текущего значения на входе раунда с первым подключом раунда.
- Вычислить наибольшее значение между результатом п.1 и значением без XOR (входом раунда).
- Вычислить однобитовую XOR свёртку между результатом п.2 и вторым раундовым подключом.
- Если значение бита свёртки равно 1, то заменить исходное раундовое значение на результат полученный в п.1.
- Если значение бита свёртки равно 0, то оставить результат на выходе раунда равным исходному значению на входе раунда без каких-либо изменений.
Расшифрование производится таким же образом, проходя раунды в обратном порядке.
Если заменить операцию XOR (за исключением п.3) на вычитание по модулю любого числа, то можно работать с блоками любого размера, в т.ч. не с двоичными числами. При этом необходимо соблюдать равномерность и случайность в создании раундовых подключей в соответствии с областью определения.
Работа исследователей была проведена на гранты Национального Научного Фонда США по программе финансирования математических наук. По их утверждению, открытие нового метода создания шифров явилось случайным побочным результатом исследований в области создания алгоритмов блочного шифрования с сохранением формата сообщений (FPE). Пока ключевого расписания к данным алгоритмам не создано, в работе предлагается использовать swap-or-not-сети для FPE-шифрования совместно с шифром AES.
P.S.
Работа авторов заслужила честь открыть конференцию CRYPTO-2012.
А на Rump-сессии в ходе закрытия конференции Серж Водене попытался сделать "закрытие" этого "открытия". В докладе 
"Конец шифрования на перетасовке карт?" он указал на уязвимость в практической реализации алгоритма, в том виде как он был предложен авторами. Он отметил, что выбор максимального значения не может быть использован для замены значений, т.к. это в некоторых случаях приводит к утечке информации об определённых битах ключа и превращению алгоритма в линейную функцию. Для спасения алгоритма он предложил реализовать идею Генри Гильберта в использовании функции выбора Xˆ ← (X + X') mod 2l.
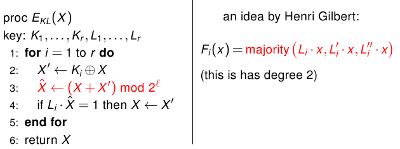
Стойкость альтернативного варианта реализации также не является строго обоснованной и уже на этапе предложения вызывает сомнения в применимости для шифрования на малых множествах.
Источник: Cryptography and Security Archive, Advances in Cryptology — CRYPTO 2012, Crypto 2012 rump session.
Unknown, вы могли бы на пальцах объяснить, что мерит часто использующаяся в криптостатьях функция Adv? Это вероятность утечки или что? Может быть, на каком-нить простейшем модельном примере...Ответ найден, хотя он слишком мудрёный. Хотелось бы на более простых функциях, чем DES. Значение параметра 1-2-8 в конце тоже непонятное. Идеальный оракул имеет Pr[A1(G)=1]=0, а «идеальный DES» имеет Pr[A1(F)=1]=1? Мы сравниваем единицу с нулём для вычисления Adv? Почему бы не взять одинаковую величину в обоих случаях? А то получается, как сравнение сапогов с пирогами.SATtva, почему Avv1vv не отрабатывает?
комментариев: 9796 документов: 488 редакций: 5664
Потому, что в местной вики-разметке написано, что отдельно стоящий символ надо брать в двойные кавычки: A1
А для их примера с DES вроде не так. Хотелось бы какое-то общее правило, чтобы было сразу понятно, какие случаи описывать через Adv.
Пример ближе к земле: есть идеальный RNG, его вборка из n бит брутфорсится за 2n-1 шагов, а есть корявый RNG, выборка n бит которого будет брутфорситься за 2m-1 шагов, где m<n. Правильно ли записывать неидеальность RNG через Adv? И если да, то как? Или вообще в такие примитивные примеры не стоит тянуть Adv-обозначения, а стоит всё писать по старинке?
Хм. Сколько тут формул написал, а не знал про это правило. Видимо, обычно нужен курсив или толстые буквы, и тогда этой проблемы не возникает. Что интересно, про воркэраунд с квотированием для данного случая тоже забыл. :)
но
Оба примера — конструкции, близкие к идеальным, но в одном случае advatange (преимущество) атакующего алгоритма равно нулю, а во втором оно почти единица. Я потому и говорю, что с чем сравнивается-то? Именно по сути, а не по форме.
комментариев: 9796 документов: 488 редакций: 5664
У DES размер блока — 64 бита, а размер ключа — 56 бит. Если перебрать все ключи, то окажется, что не все перестановки выпадают. Разница в выпадении единицы для идеальной перестановки и DES-совской как раз и составит эти 8 бит, из-за урезанного ключа по отношению к размеру блока. Тривиальный брутфорсовский различитель равен 1-28. Был бы размер ключа равен размеру блока, то при полном брутфорсе одного запроса, что к оракулу, что к DESу было бы 1 – 1 — т.е. нулевое преимущество.
Про RNG у вас мыслей нет?
комментариев: 9796 документов: 488 редакций: 5664
Там же всё написано. Чтобы дойти до такой степени различения нужно перебрать все 256 ключей на единственный запрос с одним открытым текстом и известным по отношению к нему шифртекстом. И толку иметь такой различитель после прохождения полного брутфорса? Поэтому, такие различители называются тривиальными.
Если у вас всего два выбора, то анекдот же был про Сталина на эту тему.
Adv(A1) = |Pr[A1 (RNGideal-PRF) = 1] – Pr[A1 (RNGgood ) = 1 ] – Pr[A1 (RNGbad) = 1]| = 1 – 2-(n-1) – 2-(m-1)
комментариев: 9796 документов: 488 редакций: 5664
А RNG — это PRF, а не PRP, как DES.
У идеального PRF внутреннее состояние бесконечно (не ограничено размером блока, в отличие от PRP), это как одноразовый блокнот. Для идеального PRF вы найдёте ключ с вероятностью 0 (не найдёте никакого ключа с вероятностью 1). См.
комментариев: 9796 документов: 488 редакций: 5664
В RO-PRF вы так и не найдёте никакого ключа, которым можно предсказывать дальнейшую последовательность. Даже после n запросов. Значит, после n запросов, вы с вероятностью 1 скажете — что это идеальный PRF.
Перебрали 264-8 = 256 ключей и оказалось, что часть из них успешно шифруют открытый текст в шифртекст, а некоторые 264-56 — никак.
Ссылки из вики ведут сюда. И у нас тоже.
Похоже, мы вообще о разном говорим. Ладно, чуть подробнее:
Если RNG идеальный, Бобу в среднем понадобится сделать 2n-1 запросов к OA. Если нет, то меньше: 2m-1, m<n. Стоит ли разницу между идеальным RNG и неидеальным записивать с помощью Adv-нотаций? Т.е., я могу сейчас пофантазировать, как бы это могло выглядеть, но вдруг вы сразу скажете, что я пытаюсь тянуть к этой задаче тот концепт, который здесь вообще неуместен.
И после этого мы ещё в соседней ветке gegel'я ругаем... ☹
комментариев: 9796 документов: 488 редакций: 5664
Adv(q) = maxa { Pr [Agood_RNG ⇒ 1] – Pr[Abad_RNG ⇒ 1] }
надо найти максимум.
Весь интернет перерыл в поисках того, где описано это обозначение (знаю, что оно конвенциональное в CS/крипто), а оказалось, что в самом тексте написано. Вроде обычно пишут [n]={0,1,…,n} (множество), не? Где-то в статьях по крипто попадалось даже 2[n] — это что, булеан? Но тогда 2[n] = 2n.
Почему используется знак ⇒? Это конвенциональное обозначение для «алгоритм Agood_RNG даёт положительный ответ»?
Да, это само собой.
Получается иная характеризация, чем через среднее число шагов, и при этом вроде как более детальная, поскольку разные алгоритмы могут быть по-разному хуже для разных значений q, однако, давать одно и то же среднее значение для числа шагов на угадывание. Правда, подразумевалось, что можно найти строго доказуемый оптимальный алгоритм, и тогда перебирать алгоритмы не придётся — достаточно написать строгие оценки для разных n.