Доводы в пользу квантового распределения ключей
Институт информационной безопасности, Квинслендский университет технологий, Брисбэн, Австралия. Институт квантовых вычислений, университет Ватерлоо. Кафедра комбинаторики и оптимизации, университет Ватерлоо. Институт границ теоретической физики. Кафедра физики и астрономии, университет Ватерлоо — Ватерлоо, Онтарио, Канада.
Перевод © 2009 unknown
Краткое содержание
Квантовое распределение ключей (Quantum Key Distribution — QKD) даёт возможность безопасного согласования ключей с использованием квантово-механических систем. Мы приводим доводы в пользу того, что QKD станет важной частью криптографических инфраструктур будущего. Оно может обеспечить долговременную конфиденциальность для зашифрованной информации без опоры на предположения о вычислительных возможностях. Хотя QKD всё ещё требует аутентификации для предотвращения атак "человека посредине", возможно использование или информационно-теоретической аутентификации по симметричному ключу или вычислительно стойкой аутентификации по открытому ключу: даже при использовании аутентификации с открытым ключом мы аргументируем, что QKD всё ещё обеспечивает более высокую безопасность, чем классическое согласование ключа.
1 Введение
С момента своего открытия область квантовой криптографии — и в частности квантовое распределение ключа (QKD) получила широкий технический и популярный интерес. Перспектива "безусловной стойкости" вызвала интерес публики, но часто чрезмерный интерес, проявляемый в данной области также порождал критику и анализ.
QKD — новый инструмент в наборе криптографических средств: он позволяет осуществлять безопасное согласование ключа по небезопасному каналу, что является невозможной задачей для классической криптографии (Все вычисления должны рассматриваться как имеющие место в физической системе, описываемой определёнными законами природы. Под классической криптографией мы понимаем криптографию, имеющую место в вычислительных и коммуникационных системах, моделируемых классической физикой, т.е. неквантово-механической и нерелятивистской физикой; т.е. речь идёт о процессах, описываемых вероятностными машинами Тьюринга). QKD не устраняет необходимость в других криптографических примитивах, таких как аутентификация, но может быть использовано для построения систем с новыми свойствами безопасности. По мере продолжения экспериментальных исследований мы ожидаем, что стоимость и сложности использования QKD упадут до уровня, когда системы QKD могут быть доступны для широкого развёртывания, а обращение с ними может стать предметом сертификации.
В течении всей этой публикации мы делаем упор в нашей дискуссии на квантовой криптографии в виде квантового распределения ключей (QKD). Существует множество других квантовых криптографических примитивов — приватные квантовые каналы, квантовое шифрование с открытым ключом, квантовое подбрасывание монеты, квантовые вычисления вслепую, квантовые деньги — но большинство из них требует для своего выполнения средне- или крупномасштабного квантового компьютера. С другой стороны, QKD уже было выполнено множеством разных групп, наблюдались попытки коммерциализации и его потенциальная роль в последующих инфраструктурах безопасности заслуживает серьёзных исследований.
Существует три стадии (которые иногда переплетаются) в установлении безопасных комуникаций:
1. Согласование (совместная выработка) ключа: две стороны договариваются о безопасном, совместно используемом закрытом ключе.
2. Аутентификация: позволяет стороне быть уверенной, что сообщение происходит от определённой стороны. В случае согласования ключа для избежания атаки "человека посредине" должна использоваться некоторая форма аутентификации.
3. Использование ключа: как только ключ безопасно согласован, он может быть использован для шифрования (с использованием одноразового блокнота или других шифров), дальнейшей аутентификации или других криптографических целей.
QKD — это лишь часть полной инфраструктуры информационной безопасности: две стороны могут согласовать (совместно сгенерировать) закрытый ключ, безопасность которого не зависит от вычислительных предположений и который полностью независим от какого-либо входного значения протокола.
Если мы живём в мире в котором мы можем обоснованно ожидать, что криптография с открытым ключом безопасна в кратко- и среднесрочном периоде, то комбинирование криптографии с открытым ключом для аутентификации и QKD для согласования ключа приводит к очень высокому уровню долгосрочной безопасности со всеми выгодами и преимуществами, которые мы можем ожидать от распределённой аутентификации в инфраструктуре открытого ключа.
Если мы живём в мире, где криптография с открытым ключом больше не сможет обеспечивать безопасность, мы должны вернуться обратно к классическим способам распределения ключа по приватным каналам, таким как доверенные курьеры или использовать QKD. QKD всё ещё будет требовать приватных каналов для установки ключей аутентификации. Вместо того, чтобы устанавливать краткосрочные ключи аутентификации, приватный канал может быть использован для обмена ключами, которые QKD может создавать в течении долгого периода времени. Однако, при таком положении QKD может иметь преимущество поскольку объём требуемых приватных коммуникаций значительно меньше и поскольку ключи сессий на выходе из протокола QKD независимы от ключей, переданных по приватному каналу, остаётся небольшой промежуток времени, в течении которого скомпрометированный ключевой материал может затронуть безопасность последующих сессий. Каково это преимущество на практике зависит от природы приватного канала в вопросе предположений о доверии.
Если мы живём в мире, где схемы согласования ключей на основе асимметричной криптографии подразумеваются неограниченно безопасными, то здесь имеются ограниченные аргументы в пользу QKD, но оно всё ещё представляет интерес по множеству причин. QKD создаёт случайные, независимые сеансовые ключи, которые снижают ущерб, вызываемый утечкой эфемерных ключей. Другие формы криптографии также могут быть интересны, особенно для безопасного доступа к квантовой информации если квантовые вычисления получат широкое распространение.
Экспериментальные исследования в квантовом распределении ключей продолжают улучшать удобство использования, пропускную способность и расстояние для QKD систем, а также способность предоставлять и давать возможность подвергать сертификации их физическую безопасность. Поскольку системы криптографии с открытым ключом переоснащаются новыми алгоритмами и стандартами в текущие годы, то есть и возможность внедрения QKD как нового средства, предоставляющего фундаментально новые возможности безопасности.
Аналогичные работы. Эта работа мотивирована как ответ на другие мнения по поводу роли QKD, особенно сомневающимся заметкам "Почему квантовая криптография?" Патэрсона, Пайпера и Шэка. Наша дискуссия по поводу аутентификации затрагивает шифрование и аутентификацию в тех же самых аспектах как и их работа c оптимистическим взглядом на перспективы пост-квантовой криптографии с открытым ключом; мы предоставляем дополнительную информацию по допущениям о стойкости QKD, текущем состоянии исполнения QKD и как структура QKD-сетей будет вовлекаться в технологический прогресс. Отклик проекта SECOQC также относится к связанным проблемам, с особенным вниманием, которое уделяется сетям, связанным через QKD.
Краткое содержание по главам. В ходе этой публикации мы покажем, что QKD играет важную роль в безопасности инфраструктур будущего. В секции 2 мы дадим обзор того, как работает QKD и дадим примеры того, где нужна такая высокая безопасность в главе 3. Мы опишем состояние безопасности QKD в главе 4. Затем мы обсудим другие части коммуникационной инфраструктуры: шифрование в главе 5 и аутентификацю в главе 6. В главе 7 мы обсудим некоторые ограничения QKD как они устанавливаются и как они могут быть преодолены с особенным вниманием к сетям из QKD устройств в главе 8. Мы дадим заключительные выводы в главе 9.
2 Краткое введение в QKD
В этой главе мы дадим очень краткое рассмотрение квантового распределения ключа. Более детальное рассмотрение доступно из множества источников.
В QKD две стороны, Алиса и Боб, получают некоторые квантовые состояния и измеряют их. Они связываются (все коммуникации, которые происходят далее — классические), чтобы определить, какой из их результатов измерений приводит к получению секретных битов ключа; некоторые из них отвергаются, поэтому процесс называется отсеиванием, поскольку измерительные настройки были несовместимы. Они осуществляют коррекцию ошибок и затем оценивают параметр безопасности, который указывает как много информации может быть доступно из их данных подслушивающей стороне. Если это количество выше определённого порога, то они прерывают исполнение, так как больше не могут гарантировать никакой безопасности. Если это ниже порога, то они могут применить усиление приватности для выдавливания любой остаточной информации, которую может иметь прослушивающая сторона и приходят к получению совместного секретного ключа. Некоторые из этих классических коммуникаций должны быть аутентифицированы, чтобы избежать атак "человека посредине". Некоторые части протокола могут потерпеть неудачу с несущественной вероятностью.
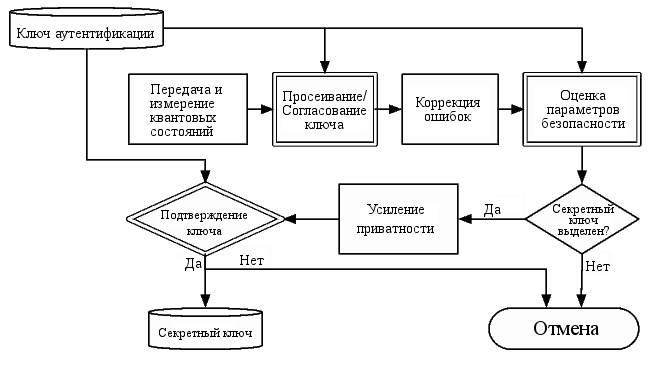
Диаграмма, описывающая квантовое распределение ключей, показана на рисунке. Этапы, обведённые в двойные рамки, требуют аутентификации классическими методами.
После того как секретный ключ установлен путём QKD, он может быть использован множеством способов. Самый распространённый подход — это использование его в качестве секретного ключа в одноразовом блокноте, чтобы достичь безусловно стойкого шифрования. Этот ключ также может быть использован в классической аутентификации в последующих раундах QKD.
Мы можем ожидать, что по мере того, как исследования в области QKD будут продолжаться, QKD-устройства будут становится всё более стойкими, лёгкими в конфигурировании, менее дорогими и малоразмерными, возможно достаточно миниатюризированными для размещения на одиночной печатной плате.
3 Кому нужно квантовое распределение ключей?
Широко распространено понятие о том, что "безопасность — это цепь; она сильна настолько, насколько сильно её самое слабое звено" и криптография, даже криптография с открытым ключом, на самом деле является одним из самых прочных звеньев в цепи. Мы не можем верить в то, что определённая вычислительно-стойкая криптографическая схема и размер параметров будут неограниченно безопасны и многие рекомендации экспертов несклонны к тому, чтобы описывать будущее за пределами ближайших тридцати лет. Хотя большинство шифруемой сегодня информации не требует тридцатилетней стойкости, иногда она нужна.
Более того, важно иметь подробный план всвязи с изменениями в технологиях безопасности. К примеру допустим, что определённые приложения, использующие RSA или криптографию на эллиптических кривых (ECC) требуют, чтобы информация была защищена в течении x лет и потребуется y лет, чтобы перевести инфраструктуру на новую криптосистему. Если крупномасштабные квантовые компьютеры, способные взламывать RSA или ECC будут созданы за z лет, то при z < x + y мы уже опоздали: нам нужно было готовить к использованию новую криптосистему задолго до того, как будет взломана старая.
Правительства, военные и разведывательственные агентства нуждаются в долгосрочной секретности. Например, британское правительство не рассекречивало отчёт 1945 года о своих попытках взломать во время второй мировой войны шифр Tunny до 2000 года, а текущие нормативы секретности США требуют держать документы в секрете до 25 лет.
Бизнес, пытающийся защитить долговременные стратегические торговые секреты может также желать долговременной конфиденциальности. Ситуации с долговременным развёртыванием, но очень специфическими коммуникациями, также являются преимуществом QKD: неудобно и дорого обновлять 1.5 миллиона банкоматов (ATM) по всему миру, даже если последний криптопротокол взломан или признан устаревшим, но QKD может обеспечить стандарты, значительно меньше меняющиеся под действием криптоанализа.
Одной особенной индустрией, требующей долговременной, гарантированной в будущем безопасности, является здравоохранение. Системы здравоохранения медленно, но необратимо становятся всё более электронными, а записи о состоянии здоровья нуждаются в приватности в течении 100 или более лет. Защита хранилищ этих данных в датацентрах — это важно; разумеется квантовое распределение ключей не предназначено для решения этой проблемы. В той же мере важно установление безопасных коммуникаций с записями медицинских данных, которые могут быть защищены информационно-теоретической безопасностью, предоставляемой квантовым распределением ключей.
Квантовое распределение ключей — не единственный способ получать информационно-теоретически стойкие ключи. Физическая транспортировка больших, случайно сгенерированных ключей — это также метод информационно теоретически стойкого распределения ключей. При цене жёстких дисков примерно 0.10$ за гигабайт, не следует недооценивать "пропускную способность грузовика, загруженного винчестерами" (хотя рост цен на топливо может противодействовать ценовой эффективности коммуникационнной системы такого рода). Такое решение приемлемо не во всех ситуациях. В некоторых случаях может оказаться невозможным заново произвести перезагрузку ключей таким способом (например спутники и космические аппараты). Это требует гарантий, что физические ключи транспортируются безопасным образом. Это также требует безопасного хранилища большого объёма ключей до их использования. QKD же требует лишь небольшого объёма ключей, ключа аутентификации, безопасно сохраняемых перед использованием. Что важнее, QKD может генерировать свежие ключи шифрования по запросу, которые должны быть сохранены только на короткий промежуток времени между генерацией ключей и шифрованием/расшифрованием сообщения, вместо того, чтобы иметь необходимость в большом хранилище секретных ключей в течении деятельности системы.
Более того, исследования в области экспериментов с квантовой информацией всё ещё находятся на ранней стадии, так что нельзя предсказать конечный результат, в виде которого будет существовать продукт, который может быть создан на основе этой технологии и эти системы могут превзойти ожидания и мечты сегодняшних инженеров и исследователей.
4 Безопасность QKD
Квантовое распределение ключей часто описывается его сторонниками как "безусловно безопасное", чтобы подчеркнуть отличие от вычислительно стойкой безопасности классических криптографических протоколов. Хотя всё ещё остаются некоторые условия, которым должны удовлетворять системы квантового распределения ключей, чтобы быть безопасными, словосочетание "безусловно стойкие" оправдано, поскольку условия не только сведены к минимуму, они в некотором смысле являются минимально необходимыми условиями. Любой безопасный протокол согласования ключей должен основываться на минимальных предположениях, чтобы безопасность не возникала из ничего: мы должны идентифицировать и аутентифицировать стороны коммуникации, мы должны иметь возможность в некотором приватном местоположении для совершения локальных операций и все стороны должны действовать в рамках законов физики.
Следующие положения описывают безопасность квантового распределения ключей, также существует множество формальных математических аргументов в пользу стойкости QKD.
Теорема 1 (Положение о безопасности квантового распределения ключей) если
A1) Квантовая механика верна, и
A2) Аутентификация безопасна, и
A3) Наши устройства обоснованно безопасны,
то с высокой вероятностью, ключ, установленный путём квантового распределения ключей, является случайным секретным ключом, независящим (с пренебрежимо малым отличием) от входных значений.
Допущение 1: Квантовая механика верна. Это допущение требует, чтобы любая прослушивающая сторона была связана законами квантовой механики, хотя внутри этой области нет дополнительных ограничений, кроме как невозможности прослушивающего получить доступ к устройствам. В частности, мы позволяем прослушивающей стороне иметь технологию квантовых вычислений произвольно больших масштабов, значительно более мощную чем это возможно при текущем состоянии дел. Квантовая механика была проверена экспериментально примерно в течении столетия с очень высокой степенью точности. Но даже если квантовая механика будет заменена новой физической теорией, это необязательно будет означать, что квантовое распределение ключей станет небезопасным: например, безопасное распределение ключей может быть достигнуто способом, аналогичным QKD, основанным исключительно только на допущении, что невозможно осуществлять коммуникации быстрее скорости света.
Допущение 2: Аутентификация является стойкой. Это допущение — один из главных вопросов, беспокоящих тех, кто оценивает квантовое распределение ключей. В порядке защиты против атак "человека посредине", большинство классических коммуникаций QKD должны быть аутентифицированы. Аутентификация может быть достигнута с помощью безусловной стойкости на основе коротких совместно используемых ключей или на основе вычислительной стойкости при использовании криптографии с открытым ключом. Мы рассмотрим вопросы аутентификации более подробно в разделе 6.
Допущение 3: Наши устройства безопасны. Конструирование реализаций QKD, которые могут быть проверяемо безопасными — это существенный вызов, над которым исследователи работают до сих пор. Хотя первые прототипы QKD-систем допускали утечку ключа по побочным каналам (они вызывали разные шумы, в зависимости от поляризации фотонов и таким образом "прототипы были безусловно безопасны против прослушивающих, которым не посчастливилось быть глухими"), экспериментальный криптоанализ привёл к лучшей теоретической и практической безопасности. Более изощрённые атаки на побочные каналы были продолжены против определённых реализаций существующих систем, но были также и предложены лучшие теоретические методы, такие как метод ловушек состояния. Доказательства безопасности, независящие от устройств, пытаются минимизировать допущения о безопасноти физических устройств. Обоснованно ожидается, что будущие теоретические и инженерные улучшения наконец дадут нам возможность получить устройства, имеющие строгие аргументы и минимальные допущения по поводу их безопасности.
5 Использование ключа: Шифрование
Наиболее обсуждаемый способ использования для ключа, сгенерированного с помощью квантового распределения ключей — это шифрование. Существуют два способа, которыми этот ключ может быть использован для шифрования.
В безусловно стойкой системе закрытый ключ из QKD используется как ключ для одноразового блокнота. Поскольку ключ информационно-теоретически стоек, то таким же будет и зашифрованное сообщение: никакой компьютер, ни квантовый, ни классический не будет способен дешифровать зашифрованное сообщение. Однако есть трудности с такой системой. Во-первых, для ключей одноразовых блокнотов должно быть организовано аккуратное хранение и управление, поскольку дважды использованные одноразовые ключи могут серьёзно повредить безопасности. Во-вторых, как мы обсудим в главе 7, физически QKD-системы пока ещё не могут генерировать одноразовые ключи с достаточно высокой пропускной способностью для того, чтобы шифровать большие сообщения в реальном времени при помощи одноразовых блокнотов.
Чтобы справиться со второй трудностью, связанной с низкой пропускной способностью QKD, предлагается использовать гибридные системы, в которых ключ из QKD расширяется при помощи классического потокового шифра или блочного шифра, такого как AES для того, чтобы шифровать большие сообщения. При такой постановке дел безопасность зашифрованного сообщения не является больше информационно-теоретической: она зависит от предположений о вычислительной стойкости сложности взлома используемого шифра. Хотя это и не идеальный случай, тем не менее это может быть также не особенно рискованно. Исторически сложилось, что криптографы могут очень успешно конструировать блочные шифры с незначительными уязвимостями: например стандарт шифрования данных DES, созданный в 1970-хх годах, более не считается безопасным всвязи с малой длиной его ключа, но при этом DES хорошо держался в течении 30 лет криптоаналитических атак. При атаках с известным открытым текстом стойкость DES была снижена с 256 до 241, но при использовании частой смены ключа эффект от атак на известном открытом тексте ограничен. Более того, не ожидается, что квантовые компьютеры окажут серьёзное воздействие на шифры: даже если алгоритм поиска Гровера подразумевает, что необходимо увеличить длину ключа в два раза, экспоненциально более быстрые атаки, ожидающиеся от алгоритма Шора и других не смогут быть применены к большинству шифров.
Даже при использовании гибридных систем, QKD предоставляет существенное преимущество над классическими способами согласования ключа: ключ из QKD не зависит ни от какого входа из протокола согласования ключей. Таким образом QKD уменьшает количество мест для атаки: после того, как ключ согласован — единственый способ атаковать такую систему — это подвергнуть шифрование криптоанализу. В противоположность этому, системы, использующие классические протоколы согласования ключа, могут быть атакованы путём влияния на вход протокола классического согласования и определения сгенерированных ключей (например, путём решения проблемы Диффи-Хеллмана). Однако при использовании QKD для генерирования коротких ключей, следует соблюдать осторожность, всвязи с эффектами конечной длины.
Гибридные QKD системы часто увеличивают безопасность в сравнении с шифрами, используемыми без QKD: подсистемы QKD обеспечивают часто обновляемый, независимый ключевой материал, который может быть использован для смены ключей в классическом блочном или потоковом шифре; при частой смене ключей мы уменьшаем риск атак на лежащий в основе используемый шифр, путём уменьшения открытых и шифртекстов, зашифрованных на одном и том же ключе.
6 Аутентификация
Квантовое распределение ключей не снимает необходимость аутентификации: наоборот, аутентификация необходима для безопасности QKD, в противном случае легко может быть осуществлена атака "человека посредине". Существует два способа осуществления аутентификации: аутентификация с открытым ключом и аутентификация с симметричным ключом. Аутентификация с симметричным ключом может обеспечить безусловно стойкую аутентификацию, но ценой необходимости иметь предустановленную пару симметричных ключей. Аутентификация с открытым ключом, с другой стороны, проще в развёртывании и обеспечивает чрезвычайно удобное распределённое доверие при комбинировании с центрами выдачи сертификатов (CA) в инфраструктуре открытого ключа (PKI). Аутентификация на открытом ключе не может сама по себе достичь информационно-теоретической стойкости. Мы однако убеждены, что даже при таком положении дел ситуация с безопасностью становится намного лучше: использование аутентификации на открытом ключе всё ещё даёт возможность получать системы, имеющие очень сильную долговременую стойкость.
Третий метод аутентификации — это использование доверенной третьей стороны, выступающей в роли активного посредника между двумя неаутентифицироваными сторонами, но это вызывает мало интереса для применения на практике. Центры сертификации, которые используются в аутентификации с открытым ключом, аналогичны доверяемой третьей стороне, но они не посредничают в аутентификации активным образом: они распространяют подписаные открытые ключи заранее, но они не участвуют в текущем протоколе аутентификации ключей. Разница в доверии между доверенной третьей стороной и центрами сертификации в аутентификации QKD меньше, чем в классическом случае, так как ключи из QKD независимы от входных значений.
6.1 Симметричная аутентификация ключей
Стороны, у которых уже есть совместно используемый закрытый ключ могут использовать безусловно стойкие коды аутентификации для своих сообщений. Первый такой метод был описан Вегманом и Картером и был усовершенствоваан для использования в QKD. Это одна из причин, по которой квантовое распределение ключей называют квантовым расширением ключа: можно взять короткий совместно используемый ключ и расширить его до информационно-теоретически безопасного большого совместно используемого ключа.
6.2 Аутентификация на открытых ключах
Хотя симметричные ключи обеспечивают безусловно стойкую аутентификацию, её сложно развёртывать, поскольку каждая пара сторон коммуникации должна совместно использовать закрытый ключ. Инфраструктура открытых ключей позволяет распределять доверие и является важной для успешной электронной коммерции. Хотя множество защитников квантовой криптографии упускают роль вычислительно стойкой аутентификации на открытых ключах в QKD, мы считаем, что аутентификация по открытому ключу будет важной в инфраструктуре квантового распределения ключей и всё ещё может давать осмысленные положения в области безопасности.
Аутентификация по открытому ключу, будучи вычислительно стойкой, имеет тенденцию оказываться взломанной неизменно раньше, чем мы ожидаем. В 1977 Райвист размышлял о том, что уйдёт 40 квадриллионов лет на решение проблемы RSA-129 (факторизации RSA-модуля размером 129 десятичных цифр), но он был взломан всего лишь 17 лет спустя. Хотя в популярной печати всё ещё периодически используются выражения вида "больше квадриллиона лет" для описания безопасности схем, построенных на проблемах теории чисел, технические рекоммендации, которые содержат более подробные нюансы стремятся не спекулировать лишком далеко в будущее за пределы 2030 года. Примечательно, что эти рекоммендации стараются "предполагать [...], что (крупномасштабные) квантовые компьютеры не станут реальностью ближайшего будущего".
Распространено ожидание, что крупномасштабные квантовые компьютеры когда-нибудь будут существовать, но по видимому нет причин в настоящее время сомневаться в их эффективности. Квантовые компьютеры однако, не единственная угроза против аутентификации с открытым ключом. Компьютеры становятся более быстрыми и новые алгоритмы помогают ускорять криптоанализ. Однако, мы не настолько пессимистичны, чтобы думать, что аутентификация с открытым ключом будет обречена. Фактически, мы верим, что аутентификация с открытым ключом будет неопределённо долго играть важную роль в безопасности коммуникаций, даже при наличии квантовых компьютеров.
Хотя существующие сегодня популярные схемы аутентификации с открытым ключом — RSA, дискретные логарифмы в конечном поле и эллиптические кривые, будут взломаны крупномасштабным квантовым компьютером, другие "постквантовые методы" не обязательно падут перед квантовыми алгоритмами и такие схемы безусловно будут разработаны. Как нам кажется, когда в будущем схемы с открытым ключом пройдут через жизненный цикл, в котором будут предложены новые примитивы, они окажутся стойкими против текущих техник атак, обоснованные параметры и размеры будут предложены, приняты и тогда компьютерные технологии и успехи криптоанализа снова изменят уровень безопасности, пока новая схема не предложит лучший компромисс. Не сложно вообразить себе 20-летний период, за который квантовое распределение ключей может претерпеть бурный рост. Структуры аутентификации на открытом ключе предоставляют широко масштабирумое использование, которое мы ожидаем от PKI и при комбинировании с квантовым распределением ключа могут дать предположительно серьёзные выгоды в безопасности. В квантовом распределении ключа, аутентификация — в качестве формы установления аутентификации по открытому ключу — нуждается в безопасности только в момент первоначального установления соединения. Как только QKD протокол выдаст некоторый секретный ключ, часть этого секрета может быть последовательно использована для аутентификации по симметричному ключу. Фактически, даже если оригинальные аутентификационные ключи будут раскрыты после первого обмена посредством QKD, ключ, полученный из QKD останется информационно-теоретически стойким. Другими словами, мы имеем следующую формулировку:
Если аутентификация не взломана в процессе первого раунда QKD, даже если она является только вычислительно стойкой, то последующие раунды QKD будут информационно-теоретически стойкими.
В противоположность этому, классические схемы обмена на основе открытых ключей не имеют этого свойства. Даже если кто-то может выполнить протокол, в котором каждый новый ключ будет передаваться зашифрованным старым ключом, прослушивающая сторона, которая записывает все коммуникации и затем взламывает первый ключ, затем может прочитать и все последующии коммуникации. В QKD новые ключи сессии полностью независимы от всех предыдущих ключей и сообщений.
7 ограничения
Два неоспоримых ограничения существуют в сегодняшних схемах квантового распределения ключей — расстояние и пропускная способность. Из-за недолговечной природы квантовомеханических состояний, существующих в процессе квантовой передачи ключей, чем на большее расстояние передаются фотоны, тем больше фотонов теряются из-за шумов и декогеренции, таким образом снижая пропускную способность, используемую для формирования секретного ключа. Расстояние и пропускная способность в генерации ключей — это компромисс, но прогресс движется в сторону увеличения общего копромисса.
Расстояние. Самые удалённые эксперименты по QKD проводились при генерации секретного ключа по оптоволоконной линии длиной свыше 184.6 км. (2006 г) и в свободном пространстве на расстоянии 144 км с пропускной способностью 12.8 бит в секунду. Такое расстояние в свободном пространстве считается достаточным для связи между любыми двумя точками Земли посредством орбитальных спутников и вероятно будет являться задачей предложенных экспериментов.
Квантовые репитеры (повторители) могут также преодолевать ограничения в расстояниях, допуская совместное использование квантовых состояний между удалёнными сторонами. Хотя такие системы пока ещё не используются, их легче создать, чем полномасштабные квантовые компьютеры; есть теоретический и практический прогресс в их разработке.
Пропускная способность в выработке ключей. Хотя в экспериментах на дальние дистанции были получены очень низкие значения пропускной способности в выработке ключей, на более коротких дистанциях были продемонстрированы более высокие скорости выработки ключей. Экспериментальные группы достигли выработки ключей свыше 4 Мегабит в секунду по 1-км волокну и 1 Мегабиту в секунду на 20-километровом расстоянии. Эти значения пропускной способности близко подходят к тому, что требуется для защиты реальных каналов связи.
Когда QKD-ключ используется для шифрования, текущие значения скорости выработки ключевого материала могут быть недостаточны для шифрования одноразовым блокнотом и потребуются гибридные схемы, в которых QKD ключ может быть использован в качестве закрытого ключа для алгоритмов симметричного шифрования, таких как AES. Однако, как мы показали в главе 5, даже гибридные QKD-системы предоставляют повышенный уровень безопасности по сравнению с классическим согласованием ключа, поскольку ключи, генерируемые QKD независимы от любого входного значения процедуры согласования ключей и поскольку многие алгоритмы симметричного шифрования устойчивы к атакам квантовых компьютеров. Ключевой материал может быть подвержен нежелательным искажениям, если противник будет вносить возмущения в квантовый канал, но такой противник никак не сможет повлиять на безопасность согласования ключей.
8 QKD сети
По мере прогресса QKD-технологии, структуры развёртывания QKD-систем будут прогрессировать в порядке прохождения четырёх стадий уменьшения ограничений расстояния и увеличения коммерческой применимости:
1. Линии связи точка-точка: Два QKD устройства, напрямую соединённые на относительно короткой дистанции.
2. Сети с оптическими переключателями: Множество QKD-устройств организованы в сеть, допускающую взаимодействие различных пар. Оптические переключатели однако не увеличивают расстояние связи. Переключатели (свитчи) не обязаны быть доверяемыми. Один из примеров такой сети — это квантовая сеть DARPA.
3. Сети с доверяемыми повторителями: Множество QKD-устройств объединено в сеть. Промежуточные узлы в сети могут выступать как классические повторители, ретранслирующие информацию между удалёнными узлами. Ретранслирующие узлы обязаны быть доверямыми, однако уровень доверия может быть снижен, если отправляющая сторона использует схему разделения секрета. Такой тип QKD-сетей может быть использован в случаях, когда оператор сети является и её пользователем, например банк может создать сеть между множеством филиалов, каждый из которых является доверямым по-отдельности. Один из примеров такой сети – квантовая сеть SECOQC.
4. Сеть с полноценными квантовыми повторителями: Множество QKD-устройств объединено в сеть с квантовыми повторителями. Хотя индивидуальные узлы всё ещё ограничены по расстоянию, узлы квантовых повторителей позволяют передавать спутанность на большие расстояния, так что QKD может выполняться между удалёнными сторонами. Квантовые повторители не нуждаются в доверии и такой тип QKD-сети соответствует сценарию с провайдером сетевого доступа.
9 Заключение
Квантовое распределение ключей предлагает использовать мощь законов квантовой механики для детекирования прослушивающей стороны для установления совместно используемого ключа, который проверяемо безопасен и независим от любых других данных, предоставляемых связывающимися сторонами по аутентифицированному каналу. Безопасность этой системы не зависит от допущений о вычислительных возможностях и таким образом имеет потенциал стойкости против будущих атакующих, неограниченных в своих классических или квантовых вычислительных мощностях.
Есть много сценариев, таких как правительства, военные, службы здравоохранения, в которых информация должна оставаться безопасной 20, 50 или даже 100 лет. Использование QKD уменьшает уровень допущений о криптографической системе и позволяет получить совместный секрет, такой, что по законам квантовой механики, он не зависит ни от каких данных, включая входные значения.
Важно учитывать, как QKD разместить в более широкой криптографической инфраструктуре. При использовании аутентификаци по открытому ключу QKD обеспечивает сильную безопасность с выгодой от использования распределённой аутентификации инфрастуктуры открытого ключа; аутентификация с открытым ключом должна быть безопасна только до момента проведения QKD, но ключ, полученный из QKD будет оставаться безопасным неограниченно долго. Если аутентификация с открытым ключом невозможна, аутнтификация с совместно используемым секретным ключом также может быть использована для большей безопасности по сравнению с классическим разворачиванием ключа.
Текущие ограничения QKD — расстояние и скорость выработки ключа — будут в будущем улучшены по мере экспериментальных исследований, а квантовые повторители будут перспективны для создания полностью квантовых сетей на большие расстояния.
Мы верим, что поскольку технология продолжает совершенствоваться, QKD будет становится всё более важным средством в наборе криптографических инструментов для построения безопасных систем связи.
Благодарности
Авторы выражают огромную благодарность в помощи при обсуждении вопроса Romain Alleaume, Daniel J. Bernstein, Hoi-Kwong Lo, Alfred Menezes и Kenny Paterson. Исследование проведено при участии университета Ватерлоо, NSERC Graduate Sholarship, OCE, Canada NSERC, QuantumWorks, MITACS, CIFAR, Ontario-MRI и Sun Microsystems Laboratories.
Данные о публикации: QuantumComm 2009 Workshop on Quantum and Classical Information Security.
Источник: Cryptology ePrint Archive



комментариев: 9796 документов: 488 редакций: 5664
комментариев: 1515 документов: 44 редакций: 5786
Где-то читал (не поручусь, что правда), что якобы на создание квантового компьютера американское оборонное ведомство уже затратило больше средств, чем в своё время на программу Аполлон.
Молодёжь, получающая профильное образование по современным физике/CS/IT и идущая потом быдлокодить на плюсах вместо того, чтобы заняться квантовой информатикой будущего, вызывает у меня непонимание: за сиюминутный кусок колбасы гробится перспектива заниматься такими технологиями. Если даже квантовая информатика не восторжествует, то уж квантовая инженерия точно будет востребованной (сверхточные прецезионные техники измерения, квантовая оптомеханика — то, что активно развивается уже сейчас).
комментариев: 1515 документов: 44 редакций: 5786
Наткнулся на интересный параграф «Трудности с квантовым компьютером»1. Получается точно так, как и предполагалось: шумы давят, а они всё равно лезут. Пытаются применить метод quantum error correction, а это приводит только к ещё большему переусложнению всей системы, и что тут реально, а чему суждено остаться гипотетической теорией — большой вопрос:
На эту тему есть отличная статья, уже упоминавшаяся.
Да я просто спросил, не имея ничего против :) На том сайте действительно много интересных статей.
1То ли мне показалось, то ли правда этот сайт как-то связан с Валиевым, который занимался реальной физикой систем, подходящих для создания квантового компьютера.
комментариев: 1515 документов: 44 редакций: 5786
Пора открывать сайт quantumleaks.org :) Итак, в продолжение /comment46892 про адиабатику имеется краткое резюме из беседы с непосредственно причастными:
камешек к камешкукубит к кубиту при построении D-Wave, проверяя на каждом шаге, не поросла ли когерентность, они сразу начали скучи16ти кубит. Как именно эти 16 кубит работают, и что с ними происходит на квантовом уровне, по ходу не понимает никто, в том числе сам D-Wave.вопреки рекламному мнениюиз всей задачи распознавания образов только одна очень-очень маленькая и незначительная часть была решена собственно с помощью D-Wave, а всё остальное решалось на классических компьютерах. Эта маленькая часть, похоже, вполне могла быть успешно решена безо всяких D-Wave'ов. Короче, убедительного экспериментального пруфа практической полезности нет.2При высокой температуре направления кубитов разупорядочены. При абсолютном нуле они все направлены в одну сторону. Annealing — что-то типа изменения ориентации кубитов при изменении температуры. Более точнее не скажу, т.к. боюсь соврать [забыл], а литературу читать времени нет.
3Русскоязычные есть везде, так что перекрытие этого и вот этого списков как бы намекает, что по адиабатике тоже можно подготовить вопросы.
4До какого числа смогли дойти — не знаю.
5И даже могут свободно публиковаться в обычных журналах. Правда, тут уже могут быть как NDA, так и патенты.
комментариев: 9796 документов: 488 редакций: 5664
комментариев: 1515 документов: 44 редакций: 5786
загаживать квантовым оффтопомразвивать всюду плотно, поэтому сразу в новости6. Толком раскурить что к чему у меня не хватило ни времени, ни квалификации, потому прийдётся ограничиться общими словами с неопределённым процентом искажения истины.[вносите поправку на возможную ахинею]
По поводу автора: математик Ааронсон11 — фигура публичная (типа Шнайера), квантовые вычисления — его тема (включая PhD), как критик D-Wave'а он тоже известен, так что его мнение достаточно интересно. Действительно, видно, что не всё так просто, как это кажется из популярных новостных
мембранпорталов12. В общем, есть некоторая надежда, что у D-Wave'а либо что-то получится, либо они хотя бы внесут вклад в понимание области.P.S.: Про яд насмешило и заставило задуматься. В /comment46740 уже упоминалось о реакции Бернштейнаа тут вот такой же странный неадекват у Ааронсона. Заметил, что когда нас приглашают за общий стол, возможность отравы в еде мне тоже приходит в голову первой мыслью (хотя меня никогда не травили, и, когда я был моложе, таких мыслей никогда не возникало). Наверное, это профессиональная болезнь: везде
видеть уязвимостьподозревать подставу.6Пока переводил, чуть не сдох. Вспоминал unknown'а каждый раз и думал: вот ругался на него, а теперь читаю свой же перевод и там те же самые проблемы. Хочется перевести без внесения отсебятины и без вынужденной цензуры типа удаления каких-то точных смыслов, потому поначалу выходят предельно корявые предложения с ужаснейшей внеземной грамматикой. Потом ещё долго меняешь куски предложений местами, чтобы хоть как-то добиться благозвучности. Единственный способ финальной доводки — оставить текст на время, потом вернуться к нему на свежую голову и заново поисправлять так, чтобы звучало всё же по-русски, сохраняло общий смысл, а на мелкие детали забить (при этом вспоминать о том, как это было в точности сказано в ориганале, категорически запрещено!). Фразеологический оборот в последнем предложении (getting even further under my skin) так и не смог перевести: от безысходности вбил в гугл, получил
«твой дом труба шатал»и задумался. А в соседних ветках твердят про прогресс и бесклавиатурный ввод. Хоть бы переводичик нормальный смогли сделать, и то уже хорошо было б.7Предыдущий пост — тоже его заслуга.
8Даже
9«Отпускаем» выравненные спины, и они слега расходятся в разные стороны при увеличении температуры — отходе от основного состояния [ground state] системы, которое соответствует температуре абсолютного нуля.
10Т.е. весь их массив работает как единое неделимое квантовое состояние, а не как механическая статистическая смесь разнородных, слабо скоррелированных элементов (кубитов).
11По совместительству большой приколист :) Есть и другие интересные посты в его блоге на тему квантовых вычислений, типа этого, где можно узнать кое-что интересного в том числе и из комментариев читателей к записям. Я основательно не рылся, но тех, кому не лень, агитирую. В интернетах известен тем, что предлагает 100k$ за убедительное доказательство невозможности осуществления квантовых вычислений в реальном мире.
12Где есть деление только на две градации: условно «учёные лгут» и условно «учёные уже
насилуют журналистовпутешествуют во времени».комментариев: 9796 документов: 488 редакций: 5664
Интересно, это какой-то чисто инженерный трюк: непонятно что построили, но посмотрим по результатам из чёрного ящика, получится ли производить на системе высокопроизводительные вычисления (и померять необходимое кол-во квантовых состояний)? Или они разработали какое-то отдельное теоретическое направление в адиабатических вычислениях (да ещё и держат его в секрете) и в определении условий того, как это можно перевести в эффективно квантовые?
комментариев: 9796 документов: 488 редакций: 5664
комментариев: 1515 документов: 44 редакций: 5786
Ну если как я понял Ааронсона и Жереми, то именно так, поэтому, понятно, и возникает скептицизм в научном сообществе по поводу деятельности D-Wave (хотя, надо понимать, в D-Wave тоже далеко не дураки сидят).
Я могу сильно ошибаться, но, насколько мне представляется история вопроса, адиабатические вычисления — то, что известно уже давно, и было прекрасно известно ещё до D-Wave (как одна из эквивалентных моделей квантовых вычислений), хотя, может быть, не так распиарено, как сейчас (за PR адиабатики отдельное спасибо D-Wave, да). Про «особое теоретическое направление» я ничего достоверно не могу сказать13, но я не слышал про великих теоретиков из их конторы (они как раз на эксперименте концентрируются, и экспериментаторов себе же в группы набирают). Как я понимаю, все крупные теоретики по квантовым вычислениям — не из D-Wave, так что особый теоретический прогресс мне кажется маловероятным. С таким же успехом можно предположить куда более прозаичную вещь: они надеялись, что «оно
взлетитзаработает», но не фартануло, а отступать некуда (финансы, гранты, надо отчитываться перед инвесторами и т.д.), и вот они выдвинули спасительную гипотезу «оно ещё может взлететь, т.к. запутанность в вычислительном базисе не пропадает» (доказательств чего мы, опять же, не имеем).На мой субьективный взгляд, самый фронтир по взаимодействиям — всякие non-demolition и weak measurements, о которых вы писали, но в non-demolition идёт воздействие на разные степени свободы квантовой системы (на одну действуем, а другую сохраняем), разные же базисы относятся к одним и тем же степеням свободы системы. Про weak measurement говорят, что это более интересная вещь: там можно что-то «немного померить», а потом «откатить» систему назад, к исходному состоянию. Но ключевой момент в том, что «откатить» удаётся только вероятностно, строго не в 100% случаев, поэтому, возможно, вы правы, что в QKD это может внести что-то новое и релевантное как атака, но раз штука вероятностная, её, наверно, можно оценивать и выкидывать из участия в формировании ключа, так что это не «смерть QKD» ни разу и квантовой механике тоже не противоречит. В конце концов, даже простыми измерениями с какой-то вероятностью вы будете получать правильные результаты, но дальше-то что... Ну, это так, всё на уровне спекуляций, так что считайте, что все дисклеймеры произнесены.
unknown asks what is unknown pure quantum state :D) Это когда вы чистый и квантовый :)
Наверное, вы хотели сказать, что вы не можете создать квантовое состояние, т.к. не знаете точные его параметры (а это обычные числа — параметры состояния)? Ну, типа пример: | ψ 〉 = 0.923 | 0 〉 + 0.3848 | 1 〉14. Если вы не знаете коэффициенты перед векторами | 0 〉 и
| 1 〉, то за одно измерение состояния вы их и не узнаете, это так. Однако, если у вас есть ансамбль идентичных состояний | ψ 〉, вы можете провести миллион измерений и оценить эти коэффициенты с очень хорошей точностью. Конечно, это не доказательство неклонируемости (а детсадовское рассмотрение вопроса для любознательных), т.к. есть более тонкие способы15, их рассмотрение можно найти в интернете.
Нет, вас, наверно, смутило слово «чистый» :) Нет никакого деления на «совсем квантовые состояния» (наверное, это то, что вы попытались назвать словом «чистый») и «не вполне квантовые состояния». Все состояния — абсолютно квантовые, если речь в принципе идёт о квантовой механике. Более того, это её принципиальная проблема и свойство: нет никакого мягкого перехода между классическими и квантовыми системами, а потому все измерения делятся строго на 2 совершенно разных типа: либо это квантовое взаимодействие, либо «измерение» (т.е. классическое взаимодействие), где последнее, буквально — взаимодействие с «классическим прибором», неминуемо приводящим к «коллапсу квантового состояния». Кроме того, квантовое взаимодействие — это, как правило, какая-то унитарная эволюция состояния16. Измерение же — неунитарная эволюция, она описывается формальной «стрелкой»: например, если в результате измерения исходного состояния | ψ 〉 = 0.923 | 0 〉 + 0.3848 | 1 〉 получили 0, значит, теперь у нас система находится в состоянии |0〉 (аналогично для единицы). Более того, эта стрелка — постулат, который многие считают неестественным, нарушающим логическую стройность и картину квантмеха, потому срачи по поводу неё17 не утихают столько, сколько существует сам квантмех.
Теперь, если вернуться к вопросу о чистоте. С каждым квантовым состоянием ассоциируется некоторое гильбертово пространство (постулат). В случае кубитов — двумерное, R2 [считайте это определением кубита :)]. Любому квантовому состоянию изолированной системы [одна частица в космосе, во всей вселенной, бесконечно удалённая от чего бы то ни было] ставится в соответствие вектор из этого пространства, причём принципиально ничего более подробного про состояние, чем его вектор, сказать [в нашем мире] нельзя (постулат). Соответственно, все возможные состояния системы образуют пространство состояний. Эти состояния — чистые, все они задаются векторами состояний.
Однако на практике часто приходится работать с системами, которые не изолированы от окружения (среды) и являются частью какой-то более общей системы, но мы хотим работать (и описывать) только нам интересную часть. Так вот, эта часть задаётся не вектором состояния в пространстве состояний, а положительно определённым эрмитовым оператором с единичным следом (в этом же пространстве) — оператором плотности состояния. Такие состояния называются смешанными (mixed), чтобы отличать их от чистых (pure). Для кубита такой оператор — матрица 2x2. Соответственно, оператор плотности в каком-то базисе даёт нам «матрицу плотности» (а вектор состояния в каком-то конкретном базисе — «волновую функцию»).
Как известно из курса линейной алгебры, коэффициенты разложения вектора задаются скалярным произведением вектора на элементы базиса. Например, все возможные состояния с заданной координатой — базис с векторами | x 〉. И если вы захотите представить вектор состояния (речь про системы с непрерывными переменными) в этом базисе, то коэффициентами будут выступать скалярные произведения18 〈 x | ψ 〉. Сей объект обозначают как ψ(x) = 〈 x | ψ 〉 и называют волновой функцией в координатном представлении. Понятно, что при описании чистые состояния можно рассматривать как частный случай смешанных. В частности, чистому состоянию соответствует оператор (он же и проектор) | ψ 〉 〈 ψ | (объект 〈 ψ | — тот же вектор | ψ 〉, но сопряжённый (из сопряжённого пространства), про | ψ 〉 обычно говорят что это вектор-столбец, а 〈 ψ | — что вектор-строка). Оператор же плотности в координатном базисе дёт матрицу плотности в координатном представлении — это объект 〈 x' | ψ 〉 〈 ψ | x 〉 = ρ ( x' , x ).
В тех книгах, которые пишутся мудаками, рассмотрение начинается с абсолютно вторичных объектов — волновых функций и матриц плотности в координатном представлении, потому дальше читатель уже обречён — никакой структуры за квантовой механикой он не увидит. Тут, конечно, ещё можно произнести много важных слов про то, что есть измерение, что с ним ассициируют произвольный эрмитов оператор, отуда берётся базис из собственных векторов физических величин, что такое проекторы и ортогональное разложение единицы, полнота и прочее — объяснить всё это в терминах волновых функций почти невозможно, потому мудаки просто не объясняют19, а массовые расстерлы таких горе-преподавателей у нас запрещены, потому все мучаются. Кстати, смешанное состояние всегда можно «очистить» (purify) — рассмотреть гильбертово пространство более высокой размерности, в котором нужное нам состояние будет чистым и описываться вектором, процедура назвается очищением (purification). Просьба не путать с дистилляцией квантового состояния (distillation) :)
Теперь что касается многочастичных систем. Двум квантовым системам, при их совместном рассмотрении, если у одной гильбертово пространство H1, а у другой — H2, ставится в соответствие прямое (тензорное) произведение пространств. Таким образом, если эти 2 частицы изолированы, они описываются вектором состояния совокупной системы в этом новом пространстве H12 = H1 ⊗ H2. Соответственно, если частиц 5, то будет 5 тензорных произведений, что для кубитов даёт 25 = 32, т.е. все наши матрицы плотности для такой системы будут 32x32, а вектора — столбики из 32ух чисел20. Как вы догадались, закон роста размерности впечатляющий: для 1024ёх кубитов, кажется, получаем число 21024 — больше, чем атомов во Вселенной (?). Казалось бы, в мире нет никаких материальных носителей, на которых можно записать коэффициенты представления векторов и матриц в столькимерном пространстве. И вот на таких векторах состояния работают те самые алгоритмы факторизации, которые факторизовывают ваши ключи. Вроде как есть даже тезис Дойча о том, что это вряд ли возможно, а если и возможно, то, наверно, многомировая интерпретация квантмеха имеет в себе какую-то основу :) Как видите, вопрос по сути философский и глубокий: возможны ли такие состояния в мире и операции над ними или нет.
Если наши две системы независимы, то их вектор состояния — проямое произведение состояний (ставлю индексы, т.к. в общем случае состояния разные) | ψ1 〉 ⊗ | ψ2 〉. Ну, аналогично для операторов плотности будет. А если системы связаны, то состояние совокупной системы не факторизуется на тензорное произведение состояний подсистем. Так вот те, которые факторизуются (по операторам плотности), называются тривиально сепарабельными, а те, которые нет — сепарабельными (если их можно представить в виде выпуклой суммы прямых тензорных произведений операторов плотности подсистем) или запутанными (если даже так представить нельзя). Если состояние совокупной системы чистое, то можно показать, что всё упрощается: если вектор совокупной системы представляется в виде прямого произведения векторов подсистем, мы имеем сепарабельное (separable) состояние (не надо рассматривать выпуклые суммы), иначе — запутанное (entangled, ещё иногда переводят как перепутанное или сцепленное). Понятно, что вы совокупное пространство можете по-разному разбить на подпространства, в которых, в свою очередь, по-разному выбрать базисы. Вот, вычислительный базис и энергетический, про которых идёт речь в новости — примеры таких базисов.
Я не знаю какая тут связь между проблемами клонирования и запутанности «на уровне основ», это слегка про разные вещи, хотя при наиболее оптимальном (хотя и не идеальном, конечно же) клонировании запутанные состояния используются (entanglement cloner).
Принцип неопределённости тут вообще напрямую ко всему вышесказанному не относится никак. Для него цепочка рассуждений примерно такая: с каждой физической величиной (постулируется, что она есть и измерима) ассоциируется эрмитов оператор в пространстве состояний системы. При разложении вектора состояния системы по собственным векторам оператора физической величины мы получаеми коэффициенты. Квадраты модулей этих коэффициентов задают вероятности получения тех значений физической величины, которые ассоциированы с этими собственными векторами (на каждый вектор по одному значению).
Далее возникает проблема курицы и яйца: откуда изначально в нашем аксиоматическом построении взять матрицы для операторов величин, и решается она так: постулируется, что коммутатор для операторов координаты и импульса равен произведению мнимой единицы на постоянную Планка: [ q, p ] = qp – pq = ih (над q и p должны стоять шяпки, т.к. это операторы). Оказывается, постулирования коммутатора достаточно, чтобы вывести явный вид для матриц операторов q и p, причём оператор импульса в координатном представлении даёт ту пресловутую волну Де-Бройля, про которую есть много звездения в быдлокурсах и быдлокнигах по якобы основам и истории квантмеха. Оператор любой другой физической величины раскладывается в ряд Тейлора или Лорана по степеням qn pm, так что автоматически получаем матрицы для всех операторов. Там есть кое-какой произвол, но он уничтожается конвенцией по принятию так называемого правила соответствия Вейля.
Так вот, соотношением неопределённостей Гайзенберга21 называют выражение для коммутатора [ q, p ] = ih. Из этого коммутатора можно вывести соотношение между дисперсиями для координаты и импульса и увидеть, что оно ограничено Планком, что как раз и соответствует невозможности точно померить импульс и координату вместе22. Более общо если говорить, вы не можете одновременно и точно померить значения двух величин в квантовом состоянии, каких бы то ни было, если их операторы не коммутируют, так что соотношение неопределённостей между тем-то и тем-то — тоже рабочий термин, много их короче... этих соотношений.
Есть ещё понятия квазиклассических квантовых состояний. Это те, которые минимизируют соотношение неопределённостей (т.е. соотношения между дисерсиями координаты и импульса «минимальны», неравенство превращается в равенство). Такие состояния по свойствам ближе всего к классической механике23.
В общем, нет там ничего сложного, и в базовом уровне при нормальном подходе всё это можно объяснить в терминах введения аксиоматики поверх линейной алгебры, которую учат все первокурсники (читай «вчерашние школьники») технических, экономических и естественнонаучных специальностей. С другой стороны, объяснить совсем с нуля в одном абзаце трудно — опираться вообще не на что. Чтобы говорить, нужно для начала иметь хотя бы общую базу — систему постулатов квантмеха, тогда всё остальное будет легко и просто пояснить. Вот ради этой базы я статью и затеиваю, которая в процессе.
13И, вообще, надо понимать, что в квантовых вычислениях я разбираюсь раз в 100 хуже, чем в QKD, хотя никогда не изучал и не занимался ни тем, ни этим.
14Сумма квадратов коэффициентов должна быть равна единице в нормированном состоянии, тогда их квадраты — это вероятности получения значений 0 и 1 в эксперименте.
15Ну и плюс есть вопрос клонирования состояний, про которые что-то известно, но не всё — например, в QKD именно такой случай.
16Эта эволюция описывается действием унитарного оператора на вектор состояния, что переводит одно состояние в другое (это эквивалентно уравнению Шредингера).
17Равно как и по поводу трактовки вероятностной природы квантовой механики.
18В унитарном пространстве скобочки для скалярного прозиведения делают квадратными по правилам математики, но в квантмехе вместо запятой принято ставить вертикальную палку.
19В ландавшице вы это не найдёте, в доступных книгах с магазинов — тоже, но редкие исключения есть.
20Как видите, для большого числа кубит с матрицами будет тяжеловато работать; наверное, поэтому пытаются теорию категорий туда присобачить.
21На уровне профессионального подхода и современных научных статей.
22Это то, что в быдлокнигах подразумевают под соотношением неопределённостей.
23В классической механике все операторы физических величин коммутируют, а соотношение неопределённостей (коммутатор) равно [ q, p ] = 0.
комментариев: 9796 документов: 488 редакций: 5664
Думаю она окажется весьма полезной. Может когда-нибудь будет даже оригинальная (в хорошем смысле этого слова) книга.
Для вас это всё возможно повседневность. А при попытке вникнуть со стороны кажется удивительной и красивой моделью (пока не знать где там всякие оборотные стороны).
Ааронсон пытается вроде как по простому объяснить, что такое квантовые деньги, но не владея матчастью я совершенно не осилил, даже на уровне мурзилки:
Он говорит о чём? Если совсем для "квантовых хомячков"? Мне не увязать это с теми основами, что вы изложили (хотя естественно там до фига всего надо знать и изучать, в хороших первоисточниках).
Стал гуглить термин unknown quantum pure state, он часто находится, даже в названиях работ. Ваши объяснения только больше запутали, ну как бы понятно "я знаю, что ничего не знаю", и не зная основ, смешно делать какие-то догадки, даже поверхностные. Короче, работать надо с этим как со своей областью, регулярно считать, следить и пр, иначе бесполезное занятие. Может ваша публикация что-то исправит в общем понимании вопроса. Сбор информации о D-wave — весьма любопытный эксклюзив, за него тоже спасибо.
комментариев: 1515 документов: 44 редакций: 5786
unknown, это не удивительно! Вы правы, там всё на уровне мурзилки, но для людей типа меня, которые уже знают основы, но понятия не имеют что такое «квантовые деньги». Ааронсон не ставит целью попутно изложить квантовую механику, да и абсурдно это было бы. Изложение основ — одна глава, ну или тоненькая брошюрка (если писать пояснения и прочее, а не как математики: написали формулировку в виде логических заключений, а ты потом сиди и думай, что же она означает на самом деле). Я уже где-то упоминал, что объекты типа | 0 〉 — это не просто «такой же ноль, как ноль бит, только квантовый», это обманчивое впечатление. Более-менее полное описание того, что такое квантовые состояние, их измерения и эволюция — около 10 сухих постулатов, которые неминуемо срывают башню (это нормально) у всех, кто впервые с ними знакомится. К ним надо просто привыкнуть, продумать, пропустить через себя и принять на веру, это занимает некоторое время на размышления, и вот только потом уже можно от них отталкиваться и идти дальше. Хотя мне кажется, что раз вы разобрались с тем, что такое Tor (в смысле гомологической алгебры), квантмех для вас должен быть простой пустяк. Ну ткните пальцев в моём тексте в утверждение, которое вам вообще не понятно, даже примерно.
Этот пассаж трудный, даже для меня. Я, конечно, могу подумать, посмотреть на доказательства теорем и понять, но даже мне надо поглядеть в книги и подумать. Для начала, если говорить совсем честно, я, конечно же, никогда систематически не изучал квантовую информатику, потому мои знания абсолютно обрывочны: что-то я всё-таки узнал из книг, что-то из статей, что-то и из обсуждений с коллегами, много что стало обыденностью (т.е. я понимаю и чувствую, что это тривиально), но через себя я это так и не пропустил. Вот теорема неклонирования (естественно, этого нет ни в каких курсах квантовой механики, т.к. все они устаревшие) — пример подобного. Я много раз видел её доказательство в разных местах, но ни разу его не «осиливал». Более того, перед тем как писать предыдущий пост я очередной раз поглядел в гугле как это доказывается, посмотрел на страницу из формул и решил «да пошло оно лесом!». А вы мне теперь жалуетесь, что не осилили :)
Если совсем грубо, на уровне первых ассоциаций, то объяснение примерно такое может быть. Там же самое оптимальное выкачивание информации о квантовом состоянии — не его измерение, а квантовое взаимодействие. Оно описывается уравнением Шредингера или, эквивалентно, унитарной эволюцией. Оператор под это дело — штука наподобие U = exp( iHt/h ), где t — время, h — постоянная планка, i — мнимая единица и H — оператор Гамильтона для системы (считайте, что он задан так же, как и пространство состояний системы). Экспоненту можно разложить по времени, тогда получится сумма единицы и линейного члена, т.е. в пределе зависимость типа линейная. Может это не имеет никакого отношения к описанному в статье — просто первое, что мне пришло в голову.
Может, он зря здесь говорит unentangled (незапутанные, т.е. сепарабельные)? Я бы сказал, что дело в скорее в нескорелированности, раздельности. Раз у нас копии состояния, и эти копии идентичны (неразличимы), нет никаких корреляций между ними помимо их идентичности. Опять же, я не знаю, что в точности имел в виду Ааронсон. Могу ещё проаппелировать к своему предыдущему посту и сказать, что верно и обратное: раз у нас копии состояния, совокупное состояние двух копий системы — вектор вида | ψ 〉 ⊗ | ψ 〉, т.е. оно сепарабельное (синоним слова «незапутанное»).
А дальше уже тривиальности идут в вашей цитате:
Если вдруг мы знали алгоритм как приготовить | ψ 〉, то понятно, что мы можем повторить процедуру ещё раз и снова его приготовить (ну, взять ещё несколько электронов и применить к ним ту же процедуру, в итоге все они будут в том же состоянии). Это я почти дословно перевожу. Т.е. всё, что нам надо знать, спрятано в процедуре/алгоритме приготовления — можно сказать, это некая «классическая» абстрактная информация.
Тут тоже тривиал. Он нам говорит: давайте не будем пользоваться сложными теоремами и формулами, так как можно доказать на пальцах от противного. Вот есть у нас постулат — соотношение неопределённостей (см. мой предыдущий пост). Можно мерить координату или импульс, но не их оба одновременно. Ну, т.е. для измерения координаты есть такая процедура измерения, которая нам даёт правильный и точный ответ за одно измерение (если система в состоянии с определённой координатой, что есть частный случай состояния), либо выдаёт какие-то разные координаты с распределением вероятности ответа по ним (если состояние не с определённой координатой). Во втором случае мы можем восстановить это распределение, только имея большое число идентичный копий состояния (т.е. ансамбль), и проводя много измерений. Всё то же касается и импульса.
Потом Ааронсон говорит: давайте примем на веру, что мы можем клонировать состояния, тогда мы сможем показать, что это нарушает постулат о соотношение неопределённостей, т.е. базовую вещь квантовой механики, а, значит, исходное утверждение неверно, и клонировать нельзя.
Блин, чувствую что уже поплыл :( Или Ааронсон поплыл. Или мы оба. Или он ценой упрощения и большей доходчивости совершил ошибкуКажется, первое «интуитивное» понимание оказалось хотя и очевидным, но по сути ложным :(Но ладно, раз уж начал писать, то допишу эволюцию своего понимания :)
Тут он нам хочет типа сказать, что мы в одних копиях будем мерить импульс, в других — координату. В итоге мы восстановим точно и то и другое, а, значит, нарушим соотношение неопределённостей. Первая бага состоит в том, что это чушь, потому что состояний с определённым импульсом и координатой одновременно не бывает: если импульс имеет точное значение, то по координате имеет вероятность распределения по значениям (т.е. нет никакого одного и 100% точного значения). Аналогично и наоборот: если у нас точное знание координаты, то для значений импульса в принципе имеется только распределение по верояностям тех или иных значений. Так что если у нас даже ансамбль очень большого числа копий, мы терпим облом — от вероятности хотя бы по одной веичине (координате или импульсу) не избавиться.
Может я, конечно, туплю, но всё это какой-то абсурд. Даже допустим, что мы сейчас ничего не доказываем, а просто рассмотрели ансамбль идентичных состояний. Никто нам не запрещает его приготовить. Мы вольны производить измерения над всеми состояниями в этом ансамбле. И что? С какой стати это нарушит соотношение неопределённостей? Ансамбль каких-то заданных состояний можно получить в эксперименте. Короче, я ничего не понял.
По-моему, он тут с треском прокалывается на одной важной мелочи, или я ничего не понимаю. Пусть мы даже вообразим себе, что каким-то магическим способом можно получить знание вероятности распределения как по координате, так и по импульсу для нашего состояния. Только вот это ничего не даст: скопировать состояние всё равно не получится, потому что оно не задаётся (в общем случае) однозначно этими распределениями :) Полная информация заключена в совместной функции от координаты и импульса — функции Вигнера, которая хоть и не плотность вероятности по двум переменным по своему смыслу (иначе бы это противоречило соотношению неопределённостей), но нормирована и при сврётке (интегрировании) по одному аргументу даёт плотность вероятности по другому. Ну, типа квазивероятность. Вопрос её восстановления долгое время муссировался, это делают методами гомодинной томографии. Хотя действительно ведь, есть правда в том, что имея ансамбль большого числа идентичных состояний мы будем применять к ним гомодин и восстановим состояние с любой точностью, но это наш исходный посыл, а при чём тут соотношение неопределённостей? Я ничего не понял, надо читать статью.
Ваши вопросы меня — тоже :)
Вообще, знаете, Ааронсон математик. В блоге он пишет, что физику не изучал, т.е. может и изучал, но уже постфактум. Считает её знание полезным, но не необходимым, чтобы заниматься вычислениями. Может, здесь собака и зарыта? Просто я с математиками вживую дела никогда не имел, но это очень чудные люди. У нас все пришли с физики, так что знания квантмеха у них начинаются не столько с постулатов, сколько с куда более общих вещей... Скажу честно, я сомневаюсь, что математики, занимающиеся вычислениями вообще знают что такое гомодин и каковы методы реконструкции состояния. Я, к счастью, слегка знаю, т.к. у меня магистерская была на близкую тему, плюс шефы мои этой темой занимались. Но когда на кафедре терфиза выступал мой руководитель, а я оказался случайным слушателем, подметил, что народ (а все они ведут серьёзные курсы по теоретической физике у студентов) задавал настолько глупые вопросы, что я, хоть и сам троишник, им бы даже двойку не поставил — не дотягивали. Т.е. фундаментальное непонимание основ, не говоря уже о более специализированных вещах. Короче, я не буду удивлён, если в этих цитатах Ааронсона есть либо частичный, либо полный фейл. У математиков вообще свои грибы в голове, они говорят на неведомом нам языке. Помню, выступал на апробации, и чтобы ввести коллег в курс дела, председатель сказать «квантовое состояние — это положительный оператор со следом». Я первый раз такое определение услышал :) Ещё до этого выступал на предзащите, рассказывал и отвечал на вопросы час, объяснял как умел, на пальцах: теоретики не поняли ничего, экспериментаторы некоторые суть уловили. Как мне потом пояснил один уважаемый человек из присутствовавших, «было хорошо, что ты хотя бы на все вопросы формально что-то отвечал, а не молчал». Потом я долго ломал голову над вопросом «что же не так» и «как это могло произойти», пока меня не озарило: им это невозможно было объяснить, хотя они и занимаются элементарными частицами, и все считают, что квантмех знают. У них просто «другой» квантмех, они никогда сами не работают с состояниями, и все их знания об этих основах — пара предложений, да и ты выветрилась со студенческих лет. А если они не знают основ, суть квантовых каналов, например, уже не объяснишь. Кстати, математики квантовый канал определяют вот так: это вполне положительное отображение между двумя C*-алгебрами. Как вам такое определение? :)
Пожалуйста. Мне тоже так показалось, что эксклюзив. Поначалу хотел своими словами суть передать, но потом понял что суть не ужимается в несколько предложений, плюс я не настолько понимаю тему, чтобы пересказать своими словами.
Короче, моё исходное мнение было верным: пока нет полной спеки на кванты в виде связной статьи, все мои попытки и флуд на форуме обречены на фейл ;( Увы.
комментариев: 9796 документов: 488 редакций: 5664
spinore, спасибо за этот труд по изложению принципов квантмеха. Примерно так себе всё и представлял. Не в плане того, что можно изучить по краткому объяснению чего-то, нахватавшись верхов. А в плане того, как это всё структурировано. Даже какое-то странное чувство дежа-вю, хотя не пересекался с этой тематикой.
Боюсь только, что даже если осилить это изложение, то не удасться избавиться от ощущения, что квантмех — это просто очередная алгебра. Со своими постулатами, логическими связями, слегка переделанными под определённые нужды операторами. Поначалу может быть сложно уместить всё это в голове, чтобы правильно эти связи выстроить. Но вооружившись более подробными методичками, можно как студент-зубрила настрополиться решать эти задачи и на примитивном уровне выводить/понимать формулы. При слабой матподготовке — это будет уровень заурядного студента, при сильной — уровень математиков, "которые квантовый канал определяют вот так: это вполне положительное отображение между двумя C*-алгебрами. Т.е. на уровне подгонки физики под матабстракции, а не наоборот (использовании мат. инструментов для описания физики, хотя это уже давно устаревшее определение отношений).
Более того, подозреваю, что осилив квантмех на определённом уровне выше базового, некие деятели вполне могут писать откровенно бессмысленные работы, а владея лишь этим уровнем в их деятельности будет сложно разобраться (к вопросу о шлаковых публикациях). Нечто псевдонаучное и мутное также будет трудноотличимо.
Первый же абзац из публикации Ааронсона настораживает — оказывается квантмех он у всех такой разный, что его трудно оценить за пределами узкого круга специалистов, несмотря на то, что "выучить основы по методичке" могут студенты за один курс.
Что впрочем не удивительно, если даже в криптографии доказательства, определения, построения делаются не совсем так как в "чистой" математике.
комментариев: 1515 документов: 44 редакций: 5786
Кстати, это нетривиальный момент. Возьмём произвольное состояние кубита: | ψ 〉 = α | 0 〉 + β | 0 〉. Пусть у нас есть сколь угодно много идентичных копий этого состояния. И пусть мы осуществляем измерение. С вероятностью | α |2 мы будем получать значение ноль, а с вероятностью | β |2 — единицу, причём | α |2 + | β |2 = 1. Позволяет ли это восстановить | ψ 〉? Ответ — нет :) Судите сами: два разных состояния | ψ1 〉 = α | 0 〉 + β | 1 〉 и | ψ2 〉 = α | 0 〉 + β* | 1 〉 дали бы нам те же самые вероятности вероятности | α |2 и | β |2 :) Пространство-то унитарное (т.е. над полем комплексных чисел)!.
Утверждение, конечно, верно: есть такой тип измерения, который восстанавливает состояние, но тут уже прийдётся заземлять всеми любимую квантовую информатику в нелюбимую квантовую механику и представлять, что состояние кубита — модель чего-то более реального, например — состояния спина квантовой частицы со спином 1/2. Если измерять проекцию спина на все оси (направления) в нашем конфигурационном вещественном пространстве R3, ты мы получим плотность вероятности как функцию на сфере (т.е. плотность вероятности, зависящую от широты и долготы). Оказывается [как показал мой шеф в 1997ом году], эта плотность вероятности на сфере (спиновая томограмма) позволяет полностью восстановить квантовое состояние (спина, кубита и т.д.). Более того,
те кто занимается квантовой информатикой, об этом не знаютэта плотность вероятности — не произвольная, а некоторый фиксированный тригонометрический многочлен (другие недопустимы в квантовой механике), а потому нет никакой необходимости измерять эту плотность вероятности во всех точках сферы — достаточно померить только в нескольких, чтобы восстановить коэффициенты (они вещественные) того тригонометрического многочлена. Заметьте, то, что я вам сейчас озвучил, не написано ни в одной книжке :) Это я так, к слову о том, что такое кубит и понимание вопроса. А, между прочим, понятие кубита — первые страницы в книжках по квантовой информатике, даже в куче популярных статей излагаются, только вот копни чуть-чуть глубже, и сразу полезет такое, что хомячки развлекательных научных ресурсов взвыли бы, попытайся им такое впихнуть.Есть прямая формула связи, позволяющая получить α и β из этой плотности вероятности на сфере — выражается через такие милые вещи, как D-функции Вигнера и коэффициенты Клебша-Гордана (в народе — «клебши»). Посмотрите обязательно на эти формулы, впечатлитесь тривиальностью! Слегка контрастирует с понятностью того, что такое кубит, да? :) Умелые педагоги, конечно, могут объяснить даже такие вещи на пальцах. Короче, эти коэффициенты, если рассказывать по уму — просто коэффициенты матрицы перехода от одного базиса (в спиновой системе) к другому (с точностью до конвенций в нормировке).
Кстати, про запутанность: для спиновых состояний критерий проверки на сепарабельность известен, вроде бы, максимум для матриц 6x6, да и для этих-то матриц это стало известно совсем недавно. Казалось бы, в чём тут проблема? Ну если представляется ваш положительно определённый эрмитов оператор с единичным следом в виде выпуклой суммы прямых (тензорных) произведений других каких-то положительно определённых эрмитовых операторов с единичным следом, то состояние сепарабельно, иначе — запутанно. Это по определению. На языке матриц элементарно объясняется любому первокурснику. Как проверить такую представимость? В wiki написано:Решение NP-трудных задач уже само по себе впечатляет, но да ладно. Интереснее объяснение сего чудоного факта, там же, по ссылкеЭто
леденящий душу пиначе сказанный анекдот про студента после первых лекций по матану:— И как оно?
— Зря я в армию не пошёл.
Тут надо пояснение добавить: имелось в виду, что мы знаем, что наше приготавливаемое состояние — какое-то конкретное | ψ 〉, которое не является ни состоянием с определённой координатой — | x 〉, ни состоянием с определённым импульсом | p 〉, но мерить мы намереваемся именно их: координату и импульс. Просто если бы у нас было состояние | x 〉, мы могли бы померить координату, получить значение, и, таким образом полностью восстановить состояние за один акт измерения, причём само состояние от измерения даже бы не поменялось. Это тривиально следует из уже вышесказанного:Т.е. если разложить состояние с определённой координатой по базису из собственных векторов оператора координаты, то коэффициент у одного вектора в разложении будет единица, у других — нули. Единица — у того вектора, который соответствует текущему значению координаты.
Строго говоря, там коэффициент — комплексное число с модулем 1, но на фазу можно пока забить, т.к. эта фаза в данном случае — одна для всех коэффициентов в разложении (нули не меняются от домножения на фазовый множитель eiφ), а потому общая для всего состояния. Есть такое утверждение, что общая фаза состояния ни на что физически наблюдаемое не влияет (следствие из постулатов), и смысл есть говорить только об относительных фазах между состояниями. Вот если мы возьмём 2 состояния и рассмотрим их как одно совместное, уже будет важно, какие у них абсолютные фазы, т.к. из них можно вывести «разность фаз» между состояниями (но на общую фазу совокупного состояния потом так же аналогично можно будет забить).
Да, вы совершенно правильно понимаете, и это глубокий момент — что мы называем квантами (т.е. областью знаний, не путать с квантами — частицами). В плане чистой теории — это просто область математики, изначально инспирированная физикой. Просто кванты подняли много интересных вопросов в алгебре, функциональном анализе и не только, и до сих пор продолжают их поднимать. Те, кто занимаются именно этими вопросами, могут относить себя к занимающимися квантами — всё просто.
С другой стороны, важны цели, которые преследуются, и эти цели у «квантовых механиков» и обычных алгебраистов совершенно разные. В частности, первых мало волнует общность результатов — они сразу себя ограничивают только тем, что может наблюдаться в физике, потому обобщение ряда их утверждений их не волнует как класс (например, перенос утверждений из гильбертовых пространств в банаховы или что-нить в том духе). К тому же там своя идеология о том, что «полезно», «интересно», «нужно» и «достойно изучения». Например, всякие квантовые протоколы, квантовая информатика, QKD, квантовые вычисления, нахождение спектров в потенциалах (решений уравнений Шредингера), вопросы с неравенствами Белла и прочее — всё это годно. Плюс имеется подпитка новыми задачами в связи с экспериментами, откуда выводится «релевантность» решаемых задач. Обычных алгебраистов все эти вопросы интересуют мало, даже если есть прозрачная формулировка важных задач на им доступном языке. Как гласит известное утверждение, «квантовая механика — это теория линейных операторов в гильбертовом пространстве и ничего более». Напоминает аналогию «теория чисел» vs «криптография».
Например, гауссовы состояния — легки в получении (по сравнению с другими) и оперировании в эксперименте, потому есть целая область квантовой механики/информатики для гауссовых состояний, но в ней, понятно, ценности опять же математические: общность, красота, концептуальность, изящность, минимальность при той же информативности и прочее, т.е. круг изучаемых вопросов (мои каналы туда же относятся) далеко выходит за то, что интересно экспериментаторам с такими состояниями. Кстати, поскольку в гауссовых состояниях все бракеты уже давно изгнаны, я с ними сам уже лет 5 как не работаю (у них только перые и вторые моменты рассматривают — среднее и матрицу ковариаций).
Я чаще с другим сталкивался: исследуют то, что [по мнению большинства] хотя и не лженаучно, но не стоит исследований. Но, опять же, строго не докажешь, это же интуитивное ощущение, что «там нет рыбы» — всегда есть вероятность, что кто-то однажды нароет что-то очень важное и интересное. Другая распространённая проблема — статьи на актуальные и важные темы, но откровенно слабые: 80% — перефразирование ранее извествного в качестве «вводной части», потом 10% тривиальностей в духе «мы подставили такие-то значения в формулу и получили такой-то график» и ещё 10% на заключение и список литературы.
Ну он разный, но, раз это математика, про любое утверждение можно сказать на 100% точно: оно либо верно, либо нет (в отличие от криптографии). Арифметику знают уже в 12 лет, и могут даже понять проблему простых близнецов из теории чисел, а вот её решение понять? :) Ну или давайте перефразируем какие-нибудь нетривиальные факты из теории групп как свойства матричного умножения. Матрицы же все знают :) Вот поэтому методичка — одно, монография по той же теме — другое, а текущие научные статьи — третье, и даже в
теории чиселарифметике есть огромное количество до сих пор нерешённых вопросов, хотя часть из них описана в книжках для любознательных младшеклассников.Проблема в том, что область не устоялась и продолжает активно развиваться, даже претендует на «информационно-теоретический подход к физике», ни много ни мало. Область, конечно широкая, и если излагать всё, что касается основ, будет многотомник. Разные люди занимаются разными аспектами. Кто-то — всю жизнь вопросами реконструкции состояний, другие — неравенствами Белла, третьи — всякими quantum bit commitment, четвёртые — телепортацией и т.д. Это обманчивое впечатление, что всё просто. По одним неравенствам Белла можно книгу написать: по их обобщениям, по связи с теорией скрытых параметров, с лупхолами, про попытки их обобщения на непрерывные переменные. Там много вопросов. И потому не надо думать, что я легко отвечу на любой вопрос по основам, я с ним потенциально могут только «поразбираться». Если собрать всё, что известно про пропускные способности каналов, то, пожалуй, уже несколько увесистных томов-монографий будет. Пока идёт «квантовая движуха», публикуются статьи, пишутся диссертации, получают гранты и пишут отчёты как здорово мы все идём к
коммунизмубудущему типу информатики. Лет через цать грантодающие могут осознать, что QKD непрактична и дорога, в квантовые вычисления неосуществимы, после чего закрыть денежный кран и всё: тема умрёт, как ранее умерли десятки других подобных. Ну останется в мире человек 100, которые будут по инерции что-то там исследовать и публиковать, но это уже никому не будет интересно. Если что, бум интереса к квантовой информатике уже позади (как мне кажется): самый гребень на первую часть 2000ых пришёлся.Общая проблема (и не только в этой области) в том, что аксиоматические основы мало кому нужны. Все првыкают, что есть ряд доверенных фактов, а уже как они между собой связаны, никто не беспокоится. Вы же, когда задачу по планиметрии решаете, не вспоминаете аксиоматику Евклида, как что выводилось? Так же и здесь. Ситуацию ещё только усугубляет постоянное поступление новых фактов и результатов. Вот показали, например, в какой-то статье (это я фантазирую, но что-то подобное было), что если бы не неравенства Белла, у нас бы принцип причинности нарушался или мог бы существовать протокол, по которому какая-то магия возможна, типа путешествий в прошлое. И после этого всё: при обсуждениях говорят «ну это, конечно же, невозможно, ведь иначе было бы то-то!», но вот только связное доказательство подобных фактов мало кто читал, а уж о том, как встроить это в единую аксиоматическую теорию, вообще не задумывался. У нас есть всегда выбор, что взять за постулат, что за следствие, ну или просто какую теорему после какой доказывать, на что опираться. Это же множество графов на фактах, и только
бурбакистыматематики занимаются их систематизацией в одну стройную структуру. Так что нет ничего удивительного, что Ааронсон где-то мог кинуться расхожим (хотя и верным) утверждением, не особо задумывался о степени его фундаментальности в рамках системной и полной теории.Может быть, если ещё лет 40 поизучать математику и свою область, то что-то такое и получится. Проблема в том, что самое «правильное» изложение (хотя все они эквивалентны) затрагивает слишком много областей математики. Например, о спине нет и смысла говорить, если не формулировать его в терминах теории групп (спин — генератор группы поворотов SO3). Об общей структуре надо говорить в терминах C*-алгебр, а не в терминах вчерашнего дня (хотя, чувствуют, категорный язык станет стандартом раньше, чем я выучу всё это). Про механику в непрерывных переменных надо говорить на языке симплектической геометрии, а там своих проблем хватает... А я пока не знаю ни языка теории групп, ни C*-алгебр, ни симпелктичнеской геометрии. Моя книга потому обречена быть говном, как и множество других, уже написанных «учебников».
Кстати, один деятель недавно-таки написал книжу «Symplectic geometry and quantum mechanics», где изложил первую и добавил несколько глав про собственно квантовую механику, параллельно не постеснялся изучить квантмех и правильными словами
вывести на чистую водуописать всю невзрачную историю с квантовой механикой как она есть, и как её понимали поначалу. Получилось очень здоровое, компетентное, объемлющее и правильное изложение некоторых основ квантмеха в непрерывных переменных, но на большее он замахиваться не стал. Думаю, и на эту-то книгу он пол жизни уже угрохал, а это далеко не все основы.Максимум сверху, который я мог бы себе позволить — описать пропускные способности гауссовых каналов, если добью большую часть планируемых для решения задач (пока есть процентов 5 от нужных результатов): если хотя бы это удастся сделать, то уже будет большой успех.